3.1 Introduction (서론)
프로그래밍 언어를 간결하면서도 이해하기 쉽게 기술하는 작업은 매우 어렵지만, 그 언어의 성공을 위해 반드시 필요하다.
과거 ALGOL 60과 ALGOL 68이라는 언어는 매우 간결하고 형식적인 설명을 사용했으나, 당시 사람들에게 익숙하지 않은 새로운 표기법(notation) 때문에 오히려 이해하기가 어려웠고 그 결과 두 언어 모두 널리 받아들여지지 못했다.
반대로, 어떤 언어는 너무 간략하고 비형식적인 설명 때문에 조금씩 다른 여러 방언(dialect)이 생겨 혼란이 발생하기도 했다.
언어를 설명하는 과정에서 중요한 어려움 중 하나는 이 언어 설명을 읽고 이해해야 하는 사람들이 매우 다양하다는 점이다.
• 초기 평가자(initial evaluators)
언어의 초기 평가를 담당하는 사람들이다. 새로운 프로그래밍 언어는 설계가 끝나기 전 여러 단계에서 여러 사람의 평가를 받게 되며, 이러한 평가에서 이해하기 쉬운 언어 기술이 중요하다.
• 언어 구현자(implementors)
프로그래밍 언어를 실제로 구현하는 사람들이다. 이들은 언어의 표현식(expression), 문장(statement), 프로그램 단위(program unit)의 구조뿐 아니라, 그것들이 실행될 때의 의도된 효과(intended effect)까지 정확히 이해해야 한다. 언어의 설명이 명확하고 정확할수록 구현자들의 작업 난이도가 낮아진다.
• 언어 사용자(users): 실제 프로그래밍 언어로 소프트웨어를 개발하는 프로그래머들이다. 이들은 프로그래밍 문제에 대한 해결책을 만들기 위해 언어 매뉴얼을 참고한다. 따라서 교재나 매뉴얼은 이들에게 있어 언어를 배우고 활용하는 유일한 권위적인 정보원이다.
프로그래밍 언어를 공부할 때에는 자연어(natural languages)를 공부할 때와 마찬가지로 크게 두 가지 측면으로 나누어 볼 수 있다:
• Syntax (구문): 언어의 표현식, 문장, 프로그램 단위와 같은 구조적 형태를 말한다. 쉽게 말해 언어가 작성되는 형식을 의미한다.
• Semantics (의미): 표현식, 문장, 프로그램 단위가 가지고 있는 의미, 즉 언어의 문장들이 실제로 수행할 동작을 의미한다.
Example (예시): Java의 while 문을 보면,
while (boolean_expr) statement위는 syntax(구문)이다. 이 구문에 대한 semantics(의미)는 다음과 같다:
이 문장의 Boolean 표현식(boolean_expr)이 참(true)이라면, 안쪽에 있는 statement가 수행된다. 그런 다음 다시 Boolean 표현식으로 돌아가 반복 여부를 판단한다. Boolean 표현식이 거짓(false)이면, 프로그램의 흐름이 while 구문 다음에 오는 문장으로 넘어간다.
종종 설명을 위해 syntax와 semantics를 분리하지만, 실제로는 이 둘이 밀접하게 연관되어 있다. 잘 설계된 프로그래밍 언어에서는 구문이 그 자체로 의미를 강력히 암시하는 경향이 있다.
일반적으로 semantics를 설명하는 것은 syntax를 설명하는 것보다 훨씬 어렵다. 그 이유는 syntax에 대해서는 간결하고 보편적으로 인정된 표기법(notation)이 존재하지만, semantics에 대해서는 아직 그러한 표기법이 만들어지지 않았기 때문이다.
3.2 The General Problem of Describing Syntax (구문을 기술하는 일반적 문제점)
언어(자연어든, 인공 언어든)는 특정 알파벳(alphabet)에서 나오는 문자열의 집합(set of strings)으로 볼 수 있다.
이런 문자열들을 문장(sentence) 또는 명령문(statement)이라고 한다.
언어의 syntax 규칙은 어떤 문자열들이 그 언어의 알파벳으로 구성되어 언어에 포함되는지를 결정한다.
예를 들어, 영어는 복잡한 구문 규칙을 가지고 있지만, 프로그래밍 언어의 syntax는 이보다 훨씬 간단하다.
프로그래밍 언어의 syntax를 공식적으로 기술할 때, 자주 낮은 단계의 작은 단위들을 생략하고 기술한다.
가장 낮은 단계의 문법적 단위(syntactic unit)는 lexeme(어휘소)라고 한다.
lexeme의 기술은 일반적으로 언어의 구문적 설명과는 별도의 lexical specification(어휘 규격)에서 다룬다.
프로그래밍 언어의 lexeme은 숫자 리터럴(numeric literals), 연산자(operators), 예약어(special words) 등을 포함한다.
Lexeme들은 비슷한 특징을 가진 그룹으로 나뉘는데, 예를 들어 변수, 메서드, 클래스의 이름들은 모두 identifier(식별자)라는 그룹으로 분류될 수 있다. 이 그룹을 나타내는 이름을 token(토큰)이라고 한다.
Example (예시): Java의 아래와 같은 문장이 있다고 하자.
index = 2 * count + 17;이 문장의 lexeme과 token은 다음과 같다:
LexemeToken
| index | identifier |
| = | equal_sign |
| 2 | int_literal |
| * | mult_op |
| count | identifier |
| + | plus_op |
| 17 | int_literal |
| ; | semicolon |
3.2.1 Language Recognizers (언어 인식자)
언어를 공식적으로 정의하는 방식 중 하나는 인식(recognition)을 이용하는 것이다.
인식을 이용하면, 언어에 속하는 문자열을 판별하는 기계(device) R을 만든다.
즉, R은 입력된 문자열이 해당 언어에 속하는지 아닌지를 판단하여 수락(accept) 또는 거부(reject)하는 역할을 한다.
컴파일러의 구문 분석기(syntax analyzer)는 대표적인 language recognizer이다.
모든 가능한 문장을 다 테스트하지 않고, 단지 주어진 프로그램이 그 언어의 구문 규칙에 맞는지만 검사한다.
이런 구조를 parser(파서)라고 부른다.
3.2.2 Language Generators (언어 생성기)
다른 방법은 언어의 문장을 생성(generation)하는 것이다.
이것은 마치 버튼을 누를 때마다 문장이 생성되는 장치를 의미한다.
언어 생성기는 사용자가 syntax를 이해하기 쉽게 만든다는 장점이 있지만, 컴파일러와 같이 syntax가 올바른지 검사하는 데에는 효율적이지 않다.
언어 생성기와 인식자는 본질적으로 밀접하게 연결되어 있으며, 이것이 컴파일러 이론과 프로그래밍 언어 설계에 있어서 중요한 발견이다.
3.3 Formal Methods of Describing Syntax (구문 기술의 형식적 방법)
3.3.1 Backus-Naur Form and Context-Free Grammars (배커스-나우어 형식과 문맥 자유 문법)
1950년대 중후반에 언어학자인 노암 촘스키(Noam Chomsky)와 프로그래밍 언어 연구자인 존 배커스(John Backus)는 독립적인 연구를 통해 같은 문법 기술 방식을 발견했다. 이것이 현재 가장 널리 사용되는 구문 기술 방식으로 자리 잡았다.
3.3.1.1 Context-Free Grammars (문맥 자유 문법)
1950년대 중반 촘스키는 문법을 네 가지 클래스로 구분했다.
그중 정규 문법(regular grammars)과 문맥 자유 문법(context-free grammars)이 프로그래밍 언어 기술에 매우 유용하게 쓰이게 되었다.
• 정규 문법은 주로 언어의 토큰(token)을 기술하는 데 사용된다.
• 문맥 자유 문법은 프로그래밍 언어 전체의 구문 기술에 사용된다.
촘스키는 언어학자였기 때문에 처음부터 컴퓨터 언어에 관심이 있었던 것은 아니다.
그러나 후에 그의 이론이 프로그래밍 언어 기술에 적용되었다.
3.3.1.2 Origins of Backus-Naur Form (BNF의 기원)
ALGOL 58을 설계하던 중, 배커스가 처음으로 새로운 구문 기술 방식을 발표했다.
이후 피터 나우어(Peter Naur)가 ALGOL 60을 기술할 때 이를 조금 수정했고, 그 결과 나온 것이 배커스-나우어 형식(BNF)이다.
BNF는 자연스럽고 간결한 구문 표기법이다.
프로그래밍 언어의 구문을 기술하는 가장 보편적인 방법이 되었으며, 사실상 촘스키가 제안한 문맥 자유 문법과 거의 같다.
이후부터 이 책에서 문법(grammar)은 문맥 자유 문법을 지칭한다.
3.3.1.3 Fundamentals (기본 개념)
BNF는 다른 언어를 설명하는 언어인 메타언어(metalanguage)이다.
BNF 문법에서 정의하는 규칙을 다음과 같은 형식으로 표현한다:
<assign> → <var> = <expression>• 왼쪽(LHS)은 정의되는 추상 구조를 의미한다.
• 오른쪽(RHS)은 이 구조를 정의하는 구성 요소들이다.
위 규칙은 <assign>이 <var>라는 변수 뒤에 등호(=)가 오고 그 뒤에 <expression>이 따라오는 구조로 정의된다는 의미이다.
BNF에서는 추상적 요소들을 nonterminals(비단말 기호)라 부르고, lexeme과 token은 terminals(단말 기호)라 부른다.
3.3.1.4 Describing Lists (목록의 표현)
BNF는 수학에서 쓰이는 생략 부호(...)를 사용하지 않는다. 대신, 재귀(recursion)를 통해 목록을 정의한다.
예:
<ident_list> → identifier | identifier, <ident_list>이는 identifier들의 목록을 나타낸다.
3.3.1.5 Grammars and Derivations (문법과 유도)
문법은 언어의 문장을 생성하는 규칙들의 집합이다.
문장을 생성하는 과정을 유도(derivation)라고 한다. 유도는 시작 기호(start symbol)에서 시작하여 비단말 기호를 규칙에 따라 대체하는 과정이다.
EXAMPLE 3.1 (작은 언어 문법)

이 예제는 간단한 할당 언어를 정의하며, 문장 생성 과정을 단계별로 보여준다.
3.3.1.6 Parse Trees (파스 트리)
유도 과정은 계층적 구조로 나타낼 수 있는데, 이것을 파스 트리(parse tree)라 부른다. 그림 3.1은 문장 A = B * (A + C)의 파스 트리를 나타낸다.

3.3.1.7 Ambiguity (모호성)
하나의 문장에 여러 파스 트리가 존재하면 모호(ambiguous)하다고 한다. 예제 3.3과 그림 3.2에서 모호성을 보여준다.

3.3.1.8 Operator Precedence (연산자 우선순위)
모호성을 피하려면 문법에 연산자 우선순위(precedence)를 반영해야 한다. 예제 3.4와 그림 3.3이 이를 보여준다.



3.3.1.9 Associativity of Operators (연산자 결합성)
동일한 연산자의 연속적 표현에서 어느 쪽부터 평가할지 정하는 규칙을 결합성(associativity)이라 한다. 그림 3.4는 왼쪽 결합성을 보여준다.

3.3.1.10 An Unambiguous Grammar for if-else (if-else를 위한 모호하지 않은 문법)
if-else의 모호성을 해결하는 문법을 소개한다. 예제와 그림 3.5로 그 문제점과 해결 방안을 제시한다.

3.3.2 Extended BNF (확장된 BNF, EBNF)
BNF를 보다 명확하고 편리하게 확장한 것이 EBNF이다.
주요한 확장 요소는 다음과 같다:
• 대괄호[]: 선택적 요소(optional)
• 중괄호{}: 반복 요소(iteration)
• 괄호와 ‘|’: 선택적 목록(multiple-choice options)
EXAMPLE 3.5: BNF와 EBNF의 표현 비교를 보여준다.

EBNF는 다양한 변형이 있으며, ISO 표준(ISO/IEC 14977)도 존재하지만 실제로 자주 사용되진 않는다.
3.3.3 Grammars and Recognizers (문법과 인식자)
이전에 설명한 것처럼 문법과 인식자(recognizer)는 밀접한 관계가 있다.
문법이 주어지면 그것을 인식하는 기계적 인식자를 자동으로 구성할 수 있다.
대표적인 도구로는 yacc(yet another compiler compiler)가 있다.
3.4 Attribute Grammars (속성 문법)
속성 문법(Attribute Grammar) 은 문맥 자유 문법(context-free grammar)보다 프로그래밍 언어의 구조를 더 자세히 설명하기 위해 사용하는 기술이다. 문맥 자유 문법의 확장판이라 볼 수 있으며, 특히 언어의 타입 호환성(type compatibility) 같은 규칙을 명료하게 기술할 수 있게 해준다. 속성 문법의 구체적 정의에 앞서 정적 의미론(Static Semantics) 의 개념을 명확히 할 필요가 있다.
역사적 배경(history note)
속성 문법은 광범위한 분야에서 사용되어 왔다. 구문과 정적 의미론에 대한 완전한 설명을 제공하거나, 컴파일러 생성 시스템의 입력으로 사용되었으며, 문법 기반 편집 시스템(syntax-directed editing systems), 자연어 처리 시스템 등에도 활용되었다.
3.4.1 Static Semantics (정적 의미론)
정적 의미론(static semantics)은 BNF로 설명하기 어렵거나 불가능한 언어 규칙을 다룬다.
예를 들어, Java에서는 부동소수점 타입의 값을 정수 타입의 변수에 넣을 수 없다(반대는 가능하다).
이러한 규칙을 BNF로 설명하려면 지나치게 복잡한 문법이 필요해진다.
BNF로 아예 불가능한 규칙의 또 다른 예로는, “모든 변수는 사용되기 전에 반드시 선언되어야 한다”라는 규칙이 있다.
정적 의미론은 프로그램 실행 중의 의미와는 간접적인 관계만을 가지며, 주로 프로그램의 타입 제한 같은 구문적 제약에 초점을 맞춘다.
정적 의미론이라 불리는 이유는 컴파일 시간(compile time)에 이 분석이 이루어지기 때문이다.
정적 의미론을 기술하기 위해 보다 강력한 방법으로 도널드 크누스(Donald Knuth)가 속성 문법을 제안하였다.
속성 문법은 프로그램의 구문과 정적 의미론을 모두 기술할 수 있다.
3.4.2 Basic Concepts (기본 개념)
속성 문법은 문맥 자유 문법에 다음 요소를 추가한 것이다:
• 속성(Attributes) : 문법 기호에 연결되어 있고 변수처럼 값이 할당될 수 있다.
• 속성 계산 함수(Attribute computation functions) : 문법 규칙과 연결되어 속성의 값을 계산한다.
• 술어 함수(Predicate functions) : 정적 의미론 규칙을 기술하는 데 사용되는 불리언(Boolean) 표현이다.
3.4.3 Attribute Grammars Defined (속성 문법의 정의)
속성 문법은 다음의 특성을 추가로 가진 문법이다.
• 각 문법 기호 X에는 속성 집합 A(X)가 연결된다.
A(X)는 합성 속성(synthesized attributes) 과 상속 속성(inherited attributes) 으로 구성된다.
• 합성 속성 : 파스 트리의 아래에서 위로(자식에서 부모 방향으로) 의미 정보를 전달한다.
• 상속 속성 : 위에서 아래로(부모에서 자식 방향으로), 혹은 형제 간 의미 정보를 전달한다.
• 각 문법 규칙에는 속성을 계산하는 의미 함수(semantic functions) 가 연결되어 있다.
• 술어 함수(predicate function) 는 속성들이 언어의 정적 의미 규칙을 만족하는지 여부를 검사하며, false면 구문이나 정적 의미 규칙에 어긋난다.
속성 값을 모두 계산한 파스 트리를 fully attributed 라고 부른다.
3.4.4 Intrinsic Attributes (고유 속성)
고유 속성(Intrinsic attributes) 은 파스 트리 외부에서 결정되는 리프 노드의 합성 속성이다.
예를 들어, 변수의 타입이 심볼 테이블(symbol table)에서 정해진다. 파스 트리의 초기 단계에서는 오직 리프 노드의 고유 속성만 값이 있다.
3.4.5 Examples of Attribute Grammars (속성 문법의 예제)
다음은 속성 문법을 사용하여 정적 의미론을 표현하는 간단한 예제이다.
Ada 프로시저 이름 검사 예제:
Ada 언어에서 프로시저 이름과 끝나는 이름이 일치해야 한다는 규칙은 BNF로 표현할 수 없으며, 속성 문법으로 표현할 수 있다.
<proc_def> → procedure <proc_name>[1] <proc_body> end <proc_name>[2];
Predicate: <proc_name>[1].string == <proc_name>[2].string간단한 할당문의 타입 검사 예제 (EXAMPLE 3.6):

속성 문법으로 타입을 검사하는 할당문의 예시이다.
• 문법 규칙과 의미 규칙, 술어를 정의하여 표현하였다.
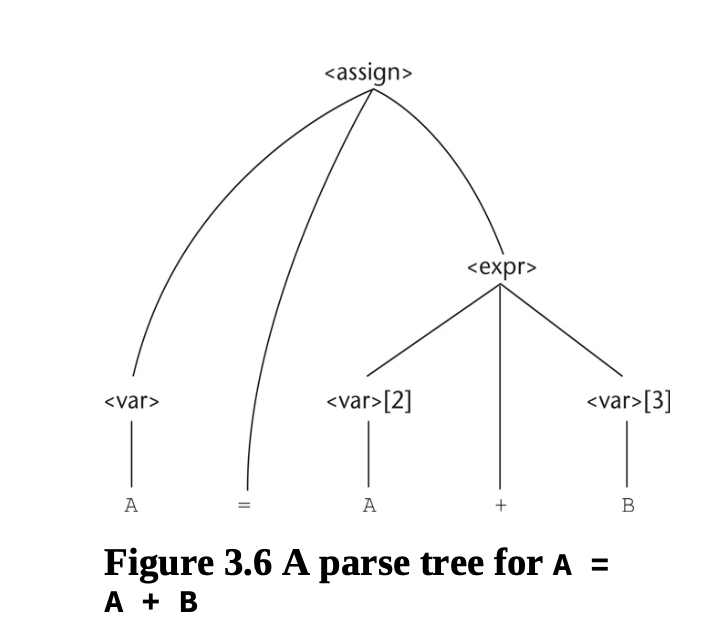
• 파스 트리 예시 (A = A + B)가 그림 3.6에 나타나 있다.
3.4.6 Computing Attribute Values (속성 값의 계산)
속성 값 계산 과정을 파스 트리를 꾸미기(decorating) 라고 한다.
상속 속성은 위에서 아래 방향으로, 합성 속성은 아래에서 위 방향으로 계산된다.
실제로는 문법 규칙에 따라 다양한 방향에서 값이 계산된다.
속성 계산의 흐름이 그림 3.7에 표현되어 있으며, 최종적으로 모든 속성이 계산된 파스 트리가 그림 3.8에 나와있다.


3.4.7 Evaluation (속성 문법 평가)
정적 의미론 규칙을 검사하는 일은 모든 컴파일러에서 필수적이다.
속성 문법을 사용하여 언어의 모든 구문 및 정적 의미를 기술하는 주된 어려움은 복잡성과 크기이다.
실제 프로그래밍 언어를 모두 표현하려면 매우 큰 문법이 필요하며, 큰 파스 트리에서의 속성 값 계산 또한 비용이 많이 든다.
하지만 덜 형식적인 속성 문법은 컴파일러 개발자에게 강력하고 일반적으로 사용되는 도구가 된다.
3.5 Describing the Meanings of Programs: Dynamic Semantics
개요
• Dynamic semantics(동적 의미론)은 프로그램 실행 시(런타임에) 각 구문이 어떻게 동작하고 결과적으로 어떤 상태(state) 변화를 일으키는지에 대한 의미를 설명한다.
• 정적 의미론(static semantics)과 달리, 동적 의미론은 프로그램이 실제로 “실행”되었을 때 벌어지는 모든 과정을 모델링하려고 한다.
• 이 절은 크게 조작적 의미론(operational semantics), 의미론적 의미론(denotational semantics), 공리적 의미론(axiomatic semantics) 이 세 가지 대표적인 기술 방법을 다룬다.
3.5.1 Operational Semantics (조작적 의미론)
핵심 아이디어
• 프로그램의 실행 과정을 “기계(또는 가상 기계)”가 한 단계씩 상태를 변화시키는 모습으로 모델링한다.
• 예: 표현식 E를 실행(평가)했을 때, 기계 상태(S)가 어떻게 (S → S')로 변하는지, 또는 문장 C가 어떤 식으로 상태를 바꾸는지를 규칙화한다.
두 가지 접근
1. Natural operational semantics(큰 단위 조작적 의미론)
• 프로그램 전체의 실행을 큰 단위로 묘사한다.
• 예를 들어, “이 프로그램을 한 번에 실행시켰을 때 최종 상태는 무엇인가?” 에 집중한다.
• 주로 증명이나 간결한 설명에 유리하다.
2. Structural operational semantics(구조적 조작적 의미론)
• 프로그램을 구문 단위별로 쪼개어, 각 문장(혹은 표현식)이 어떤 식으로 상태를 변환하는지를 세부적으로 규정한다.
• 프로그램의 구조와 평행하게 “작은 단계”로 상태 전이가 이루어지며, 이를 일련의 규칙들로 제시한다.
장점 & 단점
• 장점: 실제 컴퓨터에서 일어나는 실행 과정을 가장 직관적·직접적으로 나타낸다.
• 단점: 복잡한 언어 전체에 대해 모든 단계를 세밀하게 정의하면 상당히 방대해져서, 문서화·이해가 어려울 수 있다.
예시/그림
• 책에서는 간단한 조건문, 반복문 등에 대한 조작적 의미 규칙을 예로 든다. 예컨대 if b then S1 else S2에서 b가 참인지 거짓인지에 따라 실행 경로가 어떻게 변하는지를 단계별로 나타낸 도표나 그림이 수록되어 있다.
• 어떤 표현식이 스택 머신에서 평가되는 과정을 “스택 상태 변화”로 보여주는 식의 예제도 등장할 수 있다.
3.5.2 Denotational Semantics (의미론적 의미론)
핵심 아이디어
• 프로그램의 구문 요소(표현식, 문장, 프로그램 단위 등)를 수학적 객체(함수나 도메인)로 대응시켜, 그 “뜻(denotation)”을 함수처럼 정의한다.
• 예: E라는 표현식을 평가하는 함수를 \mathcal{M}(\cdot)라고 두고, 입력 상태를 받아서 결과값(또는 새 상태)을 산출하는 형태로 구성한다.
정의 방식
• 보통은 구문 분할(문맥 자유 문법의 구조)에 맞춰, 각 비단말 기호(nonterminal)별로 의미 함수를 정의한다.
• 재귀적으로 정의되므로, 복잡한 프로그램도 하위 요소들의 의미 함수를 모아서 전체 의미가 결정된다.
장점 & 단점
• 장점: 엄밀한 수학적 기초 위에 있기 때문에, 프로그램의 성질(예: 동등성, 종료, 불변식 등)을 논리적으로 증명하기 쉽다.
• 단점: 추상화 수준이 높아, 실제 구현이나 직관적인 면에서는 접근성이 떨어질 수 있다. 큰 언어 전체를 전부 의미론적 의미론으로 기술하려면 매우 복잡해진다.
예시/그림
• 책에서는 간단한 산술 표현식을 예로 들어, “덧셈 표현식 E1 + E2의 의미는 \mathcal{M}(E1)과 \mathcal{M}(E2)를 각각 구해 더한 값”이라는 식으로 정의하는 재귀 규칙을 보인다.
• 도식화 그림은 ‘문법 구조’와 ‘의미 함수’를 짝지어 보여주며, 최종적으로 프로그램 전체를 수학적 도메인으로 사상(mapping)하는 과정을 소개한다.
3.5.3 Axiomatic Semantics (공리적 의미론)
핵심 아이디어
• 프로그램 문장을 논리식(Hoare triple)으로 표현하고, 프로그램의 “정확성(correctness)”을 증명하기 위한 공리 및 추론 규칙을 정의한다.
• 대표적으로, {P} S {Q}라는 형태로 “문장 S를 실행하기 전 조건이 P라면, 실행 후에는 Q가 성립한다”는 논리를 쓴다. 이를 Hoare logic이라고 부른다.
주요 개념
1. 전제조건(Precondition) P
• 문장을 실행하기 전 프로그램 상태가 만족해야 하는 논리적 조건.
2. 후조건(Postcondition) Q
• 문장을 실행한 뒤 프로그램 상태가 만족해야 하는 논리적 조건.
3. 약한 선행 조건(Weakest precondition)
• 어떤 후조건 Q가 주어졌을 때, 그 Q를 만족하게 하는 가장 일반적인(“약한”) P를 의미한다.
장점 & 단점
• 장점: 논리 체계가 완비되어 있으면, 프로그램에 대한 **정확성 증명(formal verification)**이 가능하다.
• 단점: 실제 구현 수준에서 전제/후조건을 설정하거나 복잡한 언어 기능(예: 포인터, 병행성 등)에 대해 공리적 의미론을 적용하는 일은 매우 어려울 수 있다.
예시/그림
• 책에서는 if b then S1 else S2 나 while b do S 같은 구문에 대해 어떤 전제와 후조건이 필요한지를 예시로 든다.
• 그림/표에서 “조건 b가 참일 때 S1의 전후조건이 유지되는지, 거짓일 때 S2가 어떻게 작동하는지” 등을 논리 규칙으로 나타낸다.
3.5 결론 & 비교
• 조작적 의미론은 “실행 단계”를 직관적으로 추적하므로 이해하기는 쉽지만, 완전한 기술 시 상당히 방대해질 수 있다.
• 의미론적 의미론은 프로그램을 수학 함수로 대응시켜 엄밀하게 다룰 수 있으나 추상화가 높고 복잡해질 위험이 있다.
• 공리적 의미론은 프로그램의 정확성 증명에 특화되어 있으나, 실제로 모든 부분을 증명하기 위한 작업량이 매우 클 수 있다.
Summary (장 전체 요약)
• Syntax(구문) 기술:
• BNF(Backus-Naur Form)와 EBNF(Extended BNF), 문맥 자유 문법을 사용하여 프로그래밍 언어의 구조를 정의한다.
• 모호성(ambiguity)을 해소하기 위해 연산자 우선순위와 결합성 규칙을 적용하거나, 문법을 재설계한다.
• Attribute Grammars(속성 문법):
• 문맥 자유 문법에 속성(Attributes)과 의미 함수, 술어(Predicate) 등을 추가해 정적 의미론(타입 검사 등 BNF로 표현하기 어려운 규칙)을 기술한다.
• 속성은 합성 속성(Synthesized)과 상속 속성(Inherited)이 있어, 파스 트리(parse tree)에서 상·하위 노드 간 정보를 교환한다.
• Dynamic Semantics(동적 의미론):
• 3.5절에서 다룬 Operational/Denotational/Axiomatic 접근법 모두, 프로그램을 실행했을 때의 “의미”를 정의하려는 시도다.
• 각 접근법은 구체적인 실행 모델, 수학적 함수 대응, 논리적 증명 등 서로 다른 관점과 장단점을 가진다.
Review Questions
1. Define syntax and semantics.
• Syntax (구문): 프로그래밍 언어의 형식(form)을 정의하는 규칙들. 즉, “문법적으로 어떤 구조가 올바른 프로그램 문장인지”를 결정한다. 예: 변수 선언, 식의 구성, 구두점(semicolon), 괄호의 배치 등.
• Semantics (의미): 구문으로 표현된 프로그램이 실행될 때의 의미(의도, 동작, 결과)를 정의한다. 즉, “이 프로그램이 실제로 무엇을 하는지”를 설명한다.
2. Who are language descriptions for?
프로그래밍 언어를 기술한 문서는 다음을 위해 필요하다.
1. 언어 디자이너(Designer): 새로운 언어를 설계할 때, 정확하고 일관성 있게 정의하기 위해.
2. 언어 구현자(Implementor): 컴파일러나 인터프리터를 만들 때, 언어 규칙에 따라 구문 분석, 의미 분석, 실행 방식을 구현하기 위해.
3. 초기 평가자(Evaluator): 언어가 충분히 표현력이 있는지, 설계가 타당한지 피드백하기 위해.
4. 언어 사용자(User): 실제 프로그래머들이 프로그램 작성 시, 언어의 정확한 문법과 기능을 이해하기 위해.
3. Describe the operation of a general language generator.
• 언어 생성기(Language generator)는 해당 언어의 “문장들을 생성”하는 장치 혹은 모델이다.
• 예: 문맥 자유 문법에서 생성기는 시작 기호(start symbol)부터 적용 가능한 규칙을 선택해가며 문자열을 만들어낸다.
• 이 장치는 버튼을 누를 때마다 그 언어의 합법적인 문장을 하나씩 “생성”한다고 생각할 수 있지만, 실제론 무작위성이 높아 실무적 유용성은 낮다.
• 그래도 언어 생성기는 언어를 기술할 때, “이 규칙들로부터 만들어지는 문자열들의 집합 = 언어”라는 관점으로 정의에 명확성을 부여한다.
4. Describe the operation of a general language recognizer.
• 언어 인식기(Language recognizer)는 주어진 문자열이 언어에 속하는지(합법적인 문장인지)를 판별(accept/reject)하는 장치다.
• 컴파일러의 구문 분석기(parser)가 대표적 예시. 프로그램 소스(문자열) 입력 → 문법 규칙에 맞으면 accept, 아니면 reject.
• 이 장치는 언어의 문장들을 분류(filter)하며, 올바른 문장인지 아닌지 식별해낸다.
5. What is the difference between a sentence and a sentential form?
• Sentence(문장): 한 언어의 문법으로부터 완전히 유도(fully derived)된 문자열(terminal 심볼만 남은 형태). 즉, 실제로 “언어에 속하는” 최종 문자열.
• Sentential form(문장형): 유도 과정 중간에 등장할 수 있는 임의의 문자열(비단말 + 단말 기호 섞여 있음). 즉, 파생(derivation) 도중의 상태.
6. Define a left-recursive grammar rule.
• Left recursion(좌측 재귀): 문법 규칙에서 왼쪽 비단말이 자신의 오른쪽 가장 앞에 재귀적으로 등장하는 경우.
• 예: <expr> → <expr> + <term> | <term>
• 이런 규칙은 파서를 작성할 때, 특히 상향식 파싱(LL 파서)에서는 문제가 될 수 있어 보통 회피하거나 변환한다.
7. What three extensions are common to most EBNFs?
EBNF(Extended Backus-Naur Form)는 BNF를 좀 더 간결하게 쓰기 위한 확장.
1. 대괄호 [ ]: 선택적(optional) 부분을 나타낸다.
2. 중괄호 { }: 반복(0회 이상)을 나타낸다.
3. 괄호 및 파이프(|): 여러 선택사항(multiple-choice)을 묶을 때 종종 사용한다. 예: ( x | y ).
8. Distinguish between static and dynamic semantics.
• 정적 의미론(Static semantics): 프로그램 실행 전(컴파일 시점)에 검사할 수 있는 언어 규칙. 예: 타입 호환성, 변수 선언 여부 등. 속성 문법(attribute grammar) 등으로 기술할 수 있다.
• 동적 의미론(Dynamic semantics): 프로그램이 실제로 “실행”될 때 나타나는 동작이나 상태 변화를 다룬다. Operational, Denotational, Axiomatic semantics 등 기법을 통해 정의한다.
9. What purpose do predicates serve in an attribute grammar?
• Predicate는 속성 문법에서 “조건식(불리언 표현)”으로, 해당 문법 규칙이 유효하려면 참이어야 하는 조건을 명시한다.
• 예: expr.type == term.type 같은 식.
• 이를 통해 정적 의미 규칙(예: 타입 검사, 선언 규칙 등)을 기술하고, 위배되면 문법적으로는 맞아도 의미론적 오류가 발생했다고 판단한다.
10. What is the difference between a synthesized and an inherited attribute?
• Synthesized attribute (합성 속성): 자식 → 부모 방향으로 정보 전달. 예: 하위 노드(표현식)의 결과 타입이나 값이 상위 노드에 합성됨.
• Inherited attribute (상속 속성): 부모(또는 형제) → 자식으로 정보가 내려가는 형태. 예: 어떤 스코프 정보나 기대하는 타입 등 상위 문맥이 하위 노드에 전수.
11. How is the order of evaluation of attributes determined for the trees of a given attribute grammar?
• 파스 트리에서 속성 값을 올바르게 계산하기 위해서는 의존성(dependency)을 분석한다.
• 보통은 위상 정렬(topological sort) 개념을 사용. 즉, 특정 속성이 계산되기 전에 필요한 다른 속성들이 모두 계산된 상태여야 한다.
• 실무적으로는 L-속성 문법(상속 속성이 왼쪽에서 오른쪽으로만 흐르는)이나 S-속성 문법(합성 속성만 사용하는) 등을 사용하면, 계산 순서가 단순화된다.
12. What is the primary use of attribute grammars?
• 정적 의미론(static semantics)을 기술하고 검사하기 위해 쓴다.
• 즉, BNF만으로는 표현하기 어려운 타입 규칙, 선언 규칙 등을 속성과 술어로 작성하여, 컴파일 시점에 검사할 수 있도록 한다.
13. Explain the primary uses of a methodology and notation for describing the semantics of programming languages.
• 프로그래밍 언어의 의미(semantics)를 공식적으로 기술하면,
1. 언어 사용자/구현자가 정확한 동작을 이해할 수 있다.
2. 컴파일러 설계에서 구현을 체계화하거나 오류를 줄일 수 있다.
3. 프로그램 검증(correctness proof)이나 언어 설계 시, 논리적·수학적 근거를 제시할 수 있다.
14. Why can machine languages not be used to define statements in operational semantics?
• 전형적인 기계어(machine language)나 실제 컴퓨터의 상태는 너무 세부적이고 복잡(메모리, 레지스터, 하드웨어 구조 등)하므로, 언어의 의미를 간결하게 설명하기엔 비효율적이다.
• Operational semantics는 보통 “이상적인 가상 기계(abstract machine)”나 “단순화된 중간 언어”를 사용해 정의한다. 실제 기계어를 사용하면 단계가 지나치게 많고, 개념이 복잡해져 버린다.
15. Describe the two levels of uses of operational semantics.
1. Natural(큰 단위) Operational Semantics: 프로그램 전체를 한 번에(또는 큰 구문 단위별) 평가해 최종 결과 상태를 기술.
2. Structural(작은 단위) Operational Semantics: 구문 구조에 따라 단계별로(작은 조각) 상태 전이를 정의. 제어 흐름과 데이터 흐름을 미세하게 추적한다.
16. In denotational semantics, what are the syntactic and semantic domains?
• Syntactic domain: 프로그램 구문의 구조를 나타내는 집합. 예: <expr>, <stmt> 등이 표현하는 추상 구문 구조(트리).
• Semantic domain: 구문이 매핑되는 수학적 객체의 집합. 예: 정수 집합 ℤ, 불리언 집합 {true, false}, 상태(σ)의 집합 등.
17. What is stored in the state of a program for denotational semantics?
• 프로그램의 변수와 그 값(variable → value)들이 저장된다.
• 즉, 상태(state)는 일반적으로 “메모리”를 추상화한 것으로, 각 변수 이름에 대응되는 현재 값이 담겨 있다.
18. Which semantics approach is most widely known?
• 세 가지(Operational, Denotational, Axiomatic) 중, Operational semantics가 가장 직관적·널리 알려져 있다고 볼 수 있다.
• 그러나 “가장 엄밀한” 측면에서는 Denotational이, “프로그램 증명” 측면에선 Axiomatic이 사용된다.
• 일반적으로 교과서에서 Operational semantics가 많이 소개된다.
19. What two things must be defined for each language entity in order to construct a denotational description of the language?
1. 수학적 객체(Mathematical object): 그 언어 구문이 나타내는 의미 대상(예: 정수, 불리언, 함수 등).
2. 의미 함수(semantic mapping function): 구문을 해당 수학적 객체로 사상시키는 규칙(재귀적으로 정의).
20. Which part of an inference rule is the antecedent?
• Inference rule(추론 규칙)에서, 위쪽 부분(조건들, premises)이 antecedent(전제)이고, 아래쪽(결론)이 consequent이다.
──────── (조건)
결론위 “조건”이 antecedent, 아래 “결론”이 consequent.
21. What is a predicate transformer function?
• 프로그램 구문의 의미를 “전후조건” 관점에서 다룰 때, 전제조건을 후제조건과 구문에 따라 “변환”하는 함수이다.
• 예: Hoare logic에서 weakest precondition 함수 wp는 후조건 Q와 문장 S를 입력받아, 이를 만족하기 위한 전제조건 P를 산출한다.
• 즉, P = wp(S, Q)이다.
22. What does partial correctness mean for a loop construct?
• 부분적 올바름(partial correctness): 프로그램(또는 루프)이 중단(termination)을 가정하지 않고, 실행 종료 시에 올바른 결과를 낸다는 것을 의미한다.
• 즉, 프로그램이 멈춘다면 결과가 맞음. (멈출지 여부는 별도)
23. On what branch of mathematics is axiomatic semantics based?
• Axiomatic semantics는 수리 논리(Mathematical logic), 구체적으로는 술어 논리(predicate calculus)에 기반한다.
• Hoare logic 등에서 전제조건, 후조건을 논리식으로 표현하고 추론 규칙으로 다루기 때문.
24. On what branch of mathematics is denotational semantics based?
• Denotational semantics는 재귀함수 이론, 집합론, λ-계산(람다 미적분) 등 수학적 함수를 다루는 이론에 기반한다.
• 구체적으로는 재귀적 정의, 고정점 이론, 함수형 수학 모델 등이 핵심이다.
25. What is the problem with using a software pure interpreter for operational semantics?
• 소프트웨어 순수 해석기로 실제 기계 단위 동작을 전부 시뮬레이션하면,
1. 효율성 면에서 너무 느리거나
2. 하드웨어 구조(메모리, I/O 등)가 너무 복잡해서 언어 정의를 간단히 보이기 어려울 수 있다.
• 또한, 기계어 레벨의 모든 세부 단계를 명시해야 하므로 조작적 의미론을 단순 명료하게 기술하기가 힘들다.
26. Explain what the preconditions and postconditions of a given statement mean in axiomatic semantics.
• Precondition: 문장 실행 전, 프로그램 상태(변수 값들)가 만족해야 할 논리적 조건.
• Postcondition: 문장 실행 후, 프로그램 상태가 만족해야 할 논리적 조건.
• Axiomatic semantics에서 {P} S {Q}는 “P가 참인 상태에서 S를 실행하면, Q가 참이 된다”는 의미다.
27. Describe the approach of using axiomatic semantics to prove the correctness of a given program.
• 프로그램을 여러 구문 단위(문장, 블록, 루프)로 나누고, 각 문장에 대해 Hoare triple(또는 공리, 추론 규칙)을 적용하여 전제조건에서 후조건이 어떻게 유지되는지 증명한다.
• 루프의 경우 루프 불변식(loop invariant)을 찾아 증명.
• 모든 경로가 최종적으로 원하는 전제조건→후조건이 성립하면 프로그램이 “정확하다”고 증명된다.
28. Describe the basic concept of denotational semantics.
• 프로그램의 각 구문(비단말 기호)을 수학적 의미 대상(집합, 함수)에 매핑시키는 함수를 정의한다(재귀적으로).
• 이 매핑 함수는 “상태”를 입력받아 “새로운 상태” 또는 “값”을 반환한다.
• 이렇게 전체 프로그램을 순수 수학적 객체로 변환하면, 이론적인 분석·증명이 가능해진다.
29. In what fundamental way do operational semantics and denotational semantics differ?
• Operational semantics: 프로그램을 어떤 추상 기계(또는 단계적 기계)에서 실제로 실행시키는 과정을 “상태 전이”로 모델링한다. (실행 절차를 중시)
• Denotational semantics: 프로그램의 구문을 “수학적 함수”로 대응시켜, 최종 결과(또는 재귀적 평가)로 나타낸다. (수학적 매핑을 중시)
• 둘 다 런타임 동작을 다루지만, Operational은 “어떻게” 실행되는지(단계적), Denotational은 “무엇”으로 귀결되는지(함수적) 관점이 다르다.
'Book > Concepts of Programming Language' 카테고리의 다른 글
| 4. Lexical and Syntax Analysis (0) | 2025.04.05 |
|---|