1. Cache 성능 측정과 향상 기술
캐시 성능을 측정하고 분석하는 방법에는 여러 가지가 있다. 이 섹션에서는 두 가지 주요 기술을 설명한다.
1. Miss Rate 감소:
캐시 미스율을 줄여 두 개의 서로 다른 메모리 블록이 동일한 캐시 위치를 차지하지 않도록 하는 기술이다.
2. Miss Penalty 감소:
다단계 캐싱(multilevel caching)을 사용해 미스 패널티를 줄이는 기술이다.
이 기술은 1990년대 고가(10만 달러 이상) 컴퓨터에서 처음 도입되었으며, 현재는 모바일 기기에서도 사용된다.
2. CPU Time의 구성
CPU 시간이란 프로그램 실행에 필요한 CPU 실행 시간과 메모리 대기 시간의 합이다. 이를 계산하는 공식은 다음과 같다:
CPU time = (CPU execution clock cycles + Memory - stall clock cycles) * Clock cycle time
2.1 Memory-Stall Clock Cycles
Memory-stall clock cycles는 캐시 미스로 인해 발생하며, 다음과 같이 정의된다:
Memory-stall clock cycles = Read-stall cycles + Write-stall cycles
3. Read-Stall Cycles
읽기 연산에 대한 stall cycles는 다음과 같이 계산된다:
Read-stall cycles = (Reads/Program) * Read Miss rate * Read miss penalty
4. Write-Stall Cycles
쓰기 연산은 더 복잡하다. 쓰기 연산 중 다음 두 가지 stall이 발생할 수 있다:
• Write misses: 메모리 블록을 가져와야 쓰기가 가능.
• Write buffer stalls: 쓰기 버퍼가 가득 찰 때 발생.
Write-stall cycles = [(Writes/Program) * Write miss rate * Write miss penalty] + Write buffer stalls
참고:
• 쓰기 버퍼가 충분히 깊은 시스템(예: 4개 이상의 워드 지원)은 쓰기 버퍼 stall을 무시할 수 있다.
• 쓰기-스루(write-through) 캐시는 메모리로 바로 데이터를 쓰므로 write-miss가 자주 발생하지만, write-back 캐시는 블록 교체 시에만 메모리에 데이터를 쓴다.
5. Memory-Stall의 단순화
쓰기 버퍼 stall이 무시 가능한 경우, 읽기와 쓰기를 합산해 다음과 같이 계산할 수 있다:
Memory-stall clock cycles = (Memory accesses/Program) * Miss rate * Miss penalty
이를 더 단순화하면:
Memory-stall clock cycles = (Instructions/Program) * (Misses/Instructions) * Miss penalty
6. Example: Cache 성능 계산
Instruction 캐시 미스율 2%, 데이터 캐시 미스율 4%. 프로세서 CPI는 2이고, 미스 패널티는 100 클록 사이클이다.
모든 데이터 참조의 36%가 로드/스토어라고 할 때, 완벽한 캐시가 있을 경우와 비교해 성능을 계산하라.



7. Hit Time과 AMAT (Average Memory Access Time)
캐시 히트 시간(hit time)은 캐시의 크기가 커질수록 증가한다.
이는 더 큰 캐시에서 데이터를 검색하는 시간이 길어지기 때문이다. 이를 보완하기 위해 **평균 메모리 접근 시간 (AMAT)**를 사용한다:
AMAT = Hit Time + Miss rate * Miss penalty
8. Example: AMAT 계산
클록 주기 시간 1ns, 미스 패널티 20 사이클, 미스율 0.05, 히트 시간 1 사이클이라면 AMAT는?

Reducing Cache Misses by More Flexible Placement of Blocks
1. 캐시 블록 배치 정책
캐시는 메모리 블록을 특정 위치에 저장한다. 블록 배치 정책은 각 블록이 캐시에 저장될 수 있는 위치를 결정한다. 주요 배치 방식은 다음과 같다:
1. Direct-Mapped Cache (직접 매핑 캐시):
각 메모리 블록은 오직 하나의 고정된 캐시 블록에만 저장 가능하다. 이는 간단하지만 충돌이 잦아 miss rate가 높다.
• 위치 계산:
(Block number)mod(Numver of blocks in the cache)
2. Fully Associative Cache (완전 연결 캐시):
메모리 블록이 캐시 내의 아무 위치에나 저장될 수 있다.
유연성이 높아 miss rate를 줄일 수 있지만, 캐시의 모든 태그를 병렬로 검색해야 하므로 하드웨어 비용이 증가한다.
3. Set-Associative Cache (집합 연관 캐시):
Direct-mapped와 Fully associative의 절충안으로, 블록은 정해진 집합(Set) 내에서만 저장 가능하다.
각 집합은 여러 개의 캐시 블록을 포함하며, 병렬로 검색할 블록 수를 제한해 효율성을 높인다.
• 위치 계산:
(Block number)mod(Number of sets in the cache)
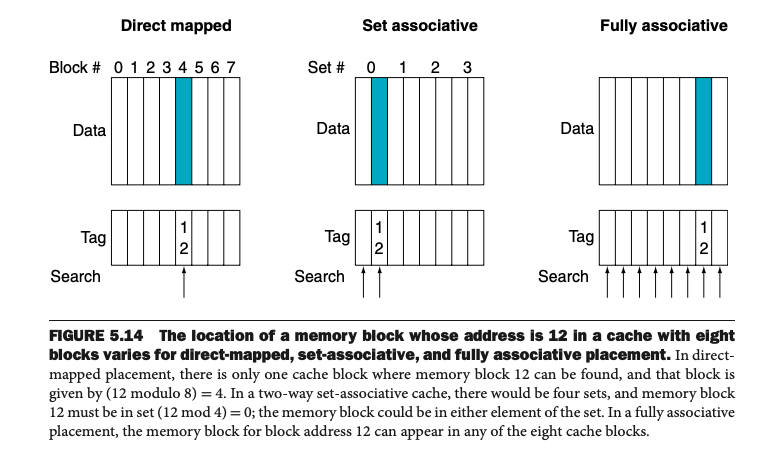
2. 그림 5.14: 세 가지 배치 방식 비교
• Direct-Mapped Cache: 블록 12는 캐시 블록 4에만 저장 가능.
• Two-Way Set-Associative Cache: 블록 12는 두 개의 블록(세트 내 두 위치) 중 하나에 저장 가능.
• Fully Associative Cache: 블록 12는 캐시 내의 어떤 블록에나 저장 가능.

3. 그림 5.15: Set-Associative 구조
1. One-Way Set Associative (Direct-Mapped): 각 세트에 하나의 블록만 포함.
2. Two-Way Set Associative: 각 세트에 두 개의 블록 포함.
3. Four-Way Set Associative: 각 세트에 네 개의 블록 포함.
4. Eight-Way Set Associative (Fully Associative): 한 세트에 모든 블록 포함.
4. 연관성(Associativity)과 Miss Rate의 관계
• 연관성이 높을수록 miss rate는 감소한다.
• 그러나 Hit Time(캐시 히트 시 검색 시간)이 증가할 수 있으므로 설계 시 균형을 맞춰야 한다.
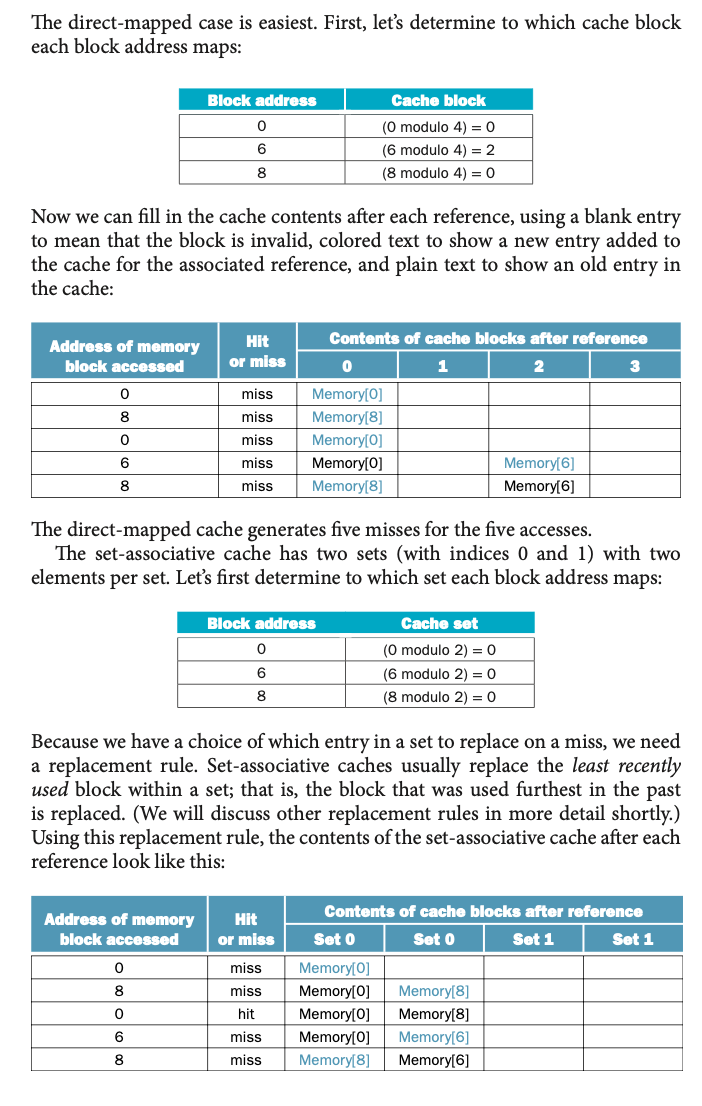
5. Example: Misses and Associativity in Caches
문제:
• 세 가지 캐시 구조: Direct-mapped, Two-way Set-associative, Fully Associative.
• 4개의 블록으로 구성된 캐시에서 0, 8, 0, 6, 8 주소 순으로 접근한다. 각 구조에서 miss 수를 계산하라.

풀이:
1. Direct-Mapped Cache:
• 블록 0 → 0, 블록 6 → 2, 블록 8 → 0.
• 결과: 5번 접근 중 5번 모두 miss.
2. Two-Way Set-Associative Cache:
• 세트 계산: (\text{Block number}) \mod 2.
• 교체 정책: Least Recently Used (LRU).
• 블록 8이 덜 최근에 사용된 블록이므로 6번 접근 시 교체 발생.
• 결과: 5번 접근 중 4번 miss.
3. Fully Associative Cache:
• 블록 0, 8, 6 순으로 적재.
• 결과: 5번 접근 중 3번 miss.

6. Miss Rate 감소에 대한 관찰
1. Fully associative cache는 가장 낮은 miss rate를 제공.
2. 그러나 2-way set-associative cache는 성능과 비용 측면에서 훌륭한 균형을 제공.
3. Miss rate는 associativity가 증가할수록 줄어들지만, Hit Time 증가가 병목이 될 수 있다.
Locating a Block in the Cache
1. Set-Associative Cache에서 블록 찾기
Set-associative 캐시에서 특정 블록을 찾는 과정은 다음과 같다:
1. Index를 이용해 세트 선택:
주소의 Index 필드는 캐시에서 해당 블록이 저장된 세트를 지정한다.
• 예: (Block number) mod (Number of sets in the cache)
2. Tag 비교:
선택된 세트에 속한 각 캐시 블록의 Tag 필드를 확인하여 요청된 블록인지 검사한다.
• 병렬 검색을 통해 속도를 높인다.
3. Block Offset 사용:
찾은 블록 내부에서 원하는 데이터를 가져오기 위해 Block Offset을 사용한다.
2. Associativity와 Miss Rate

그림 5.16은 캐시의 **연관도(Associativity)**와 데이터 미스율(Data Miss Rate) 간의 관계를 보여준다.
• 1-way (Direct-mapped): 미스율 10.3%.
• 2-way: 미스율 8.6%.
• 4-way: 미스율 8.3%.
• 8-way: 미스율 8.1%.
연관도가 증가할수록 미스율은 감소하지만, 그 효과는 점점 줄어든다.

주소의 세 가지 주요 구성 요소 (그림 5.17):
• Tag: 블록의 고유 식별자. 캐시에서 정확한 블록을 찾기 위해 사용.
• Index: 해당 블록이 속한 세트를 지정.
• Block Offset: 블록 내의 특정 데이터를 가리킴.
3. Associativity 증가의 비용
캐시 크기가 일정할 때 연관도가 증가하면 다음과 같은 변화가 있다:
1. 하드웨어 복잡성 증가:
• 각 세트에서 병렬 비교를 수행해야 하므로, 연관도가 2-배 증가하면 비교기(comparator) 수도 2-배 증가한다.
• 예: 4-way set-associative 캐시는 각 세트에서 4개의 태그를 병렬 비교.
2. Index 크기 감소:
• 연관도가 2-배 증가하면 세트 수는 절반으로 줄어들고, Index의 크기도 1 비트 줄어든다.
3. Tag 크기 증가:
• Index 크기가 줄어든 만큼 Tag 크기가 증가해 추가적인 메모리 공간이 필요하다.
4. Fully Associative Cache와 비교
• Fully Associative Cache: 모든 캐시 블록을 병렬로 검색하므로 Index 필드가 없다.
• Direct-Mapped Cache: 병렬 비교 없이, Index를 사용해 캐시 블록을 단일 위치로 직접 접근.
Choosing Which Block to Replace
1. Direct-Mapped Cache에서의 블록 교체
Direct-mapped 캐시에서는 캐시에 블록이 저장될 수 있는 위치가 하나로 고정되어 있다.
• 미스가 발생하면 해당 위치에 이미 저장된 블록은 반드시 **교체(replace)**되어야 한다.
• 교체 정책을 고려할 필요가 없으므로 설계가 간단하다.
2. Associative Cache에서의 블록 교체
Associative 캐시(fully associative 또는 set-associative)에서는 블록이 저장될 수 있는 위치가 여러 개 있다.
따라서, 미스가 발생했을 때 어느 블록을 교체할지를 결정하는 **교체 정책(replacement policy)**이 필요하다.
3. Least Recently Used (LRU) 교체 정책
**LRU (Least Recently Used)**는 가장 오랫동안 사용되지 않은 블록을 교체하는 방식이다.
• 동작 원리:
• 각 블록이 마지막으로 사용된 시간을 기록.
• 새로운 블록을 저장할 때 가장 최근에 사용되지 않은 블록을 교체.
예시:
Set-associative 캐시에서의 교체 예는 이전 예제에서 보았듯이,
Memory[0] 대신 Memory[6]을 교체한 이유가 바로 LRU 정책에 기반을 둔 것이다.
장점:
• 캐시의 효율성을 극대화.
• 자주 사용되는 데이터가 더 오래 캐시에 남을 가능성을 높임.
단점:
• 연관도가 증가할수록 구현이 복잡해짐.
• 각 블록의 사용 순서를 관리하기 위한 추가적인 하드웨어와 메모리 필요.

4. 그림 5.18: 4-Way Set-Associative Cache의 구조
그림 5.18은 4-way set-associative 캐시의 구조를 보여준다.
이 구조에서는 다음과 같은 하드웨어적 설계가 필요하다:
1. 4개의 비교기(comparators):
• 각 세트의 블록의 태그를 병렬로 검색.
2. 4-to-1 멀티플렉서:
• 비교 결과에 따라 적절한 데이터를 선택.
3. 구조 설명:
• 주소 분해:
• Tag 필드: 블록을 식별하기 위한 고유 식별자.
• Index 필드: 세트를 선택.
• Block Offset: 블록 내의 특정 데이터를 지정.
• 데이터 검색:
• 태그 비교를 통해 원하는 블록이 있는지 확인.
• 멀티플렉서를 사용해 적절한 데이터를 반환.
5. 연관성과 태그 크기
연관도가 증가할수록 캐시 설계에 추가적인 비용이 발생한다.
특히, 태그 크기 증가와 비교기 수 증가가 설계의 복잡성을 높인다.
예시: 4K 블록 캐시
• Direct-mapped:
• 세트 수 = 블록 수 = 4096, Index 크기 = 12 비트.
• 태그 크기 = 28 - 12 = 16 비트.
• 총 태그 비트 수 = 16 * 4096 = 66K 비트.
• 2-way Set-Associative:
• 세트 수 = 2048, Index 크기 = 11 비트.
• 태그 크기 = 28 - 11 = 17 비트.
• 총 태그 비트 수 = 17 * 2048 * 2 = 70K 비트.
• 4-way Set-Associative:
• 세트 수 = 1024, Index 크기 = 10 비트.
• 태그 크기 = 28 - 10 = 18 비트.
• 총 태그 비트 수 = 18 * 1024 * 4 = 72K 비트.
• Fully Associative:
• 세트 수 = 1, Index 없음.
• 태그 크기 = 28 비트.
• 총 태그 비트 수 = 28 * 4096 = 115K 비트.

6. Multilevel Caches를 사용한 Miss Penalty 감소
현대 프로세서는 **다단계 캐싱(multilevel caching)**을 통해 Miss Penalty를 줄인다.
• L1 캐시: 빠른 액세스를 위해 크기가 작고 빠름.
• L2 캐시: L1 캐시보다 크고 느림.
• 메인 메모리: 가장 느림.
효과:
• 1단계 캐시에서 미스가 발생해도, 2단계 캐시에서 데이터를 찾을 가능성이 높아 주 메모리 접근 시간을 줄인다.
7. Multilevel Cache 성능 예시
문제:
• L1 캐시 Miss Rate = 2%, Main Memory Miss Rate = 0.5%
• L1 Miss Penalty = 5ns, Main Memory Access Time = 100ns.
• 4GHz 클록 주기 (0.25ns).
풀이:
1. Main Memory Miss Penalty (400 cycles):
100ns / 0.25ns = 400 clock cycles
2. L1 Miss Penalty (20 cycles):
5ns / 0.25ns = 20 clock cycles
3. Single-Level Cache CPI:
CPI = 1 + 2% * 400 = 9
4. Two-Level Cache CPI:
CPI = 1 + (2% * 20) + (0.5% *400) = 1 + 0.4 + 2 = 3.4
속도 향상:
Speedup = 9 / 3.4 => 2.65

8. Multilevel Cache 설계 시 고려 사항
• L1 캐시는 히트 시간 감소를 최우선으로 설계.
• 작은 크기와 낮은 연관도를 사용.
• L2 캐시는 Miss Rate 감소에 초점을 맞춤.
• 더 큰 크기와 높은 연관도 사용.
Software Optimization via Blocking
1. Blocking을 이용한 캐시 성능 최적화
메모리 계층 구조(memory hierarchy)의 중요성 때문에, 많은 소프트웨어 최적화 기법이 개발되었다.
이러한 최적화는 캐시 내부 데이터를 재사용해 temporal locality(시간 지역성)를 개선하고 miss rate를 줄여 성능을 향상시킨다.
2. 배열 접근과 Blocking
배열(array)을 다룰 때, 메모리 시스템 성능을 극대화하려면 데이터 접근을 순차적으로 배치하는 것이 중요하다.
• Row-major order: 행 단위로 데이터를 저장.
• Column-major order: 열 단위로 데이터를 저장.
그러나 실제로는 행과 열을 모두 사용하는 연산이 많아, 단순히 저장 순서만 변경해서는 문제를 해결하기 어렵다.
3. Blocking의 기본 아이디어
Blocking은 배열 전체를 다루는 대신, 데이터를 작은 블록(block) 단위로 나눠 작업한다.
• 목표: 데이터가 캐시에 적재된 상태에서 최대한 많이 활용해 캐시 교체 전까지 miss를 최소화.
• Temporal Locality: 한 번 사용한 데이터를 반복해서 사용.
• Spatial Locality: 한 번 적재된 블록의 데이터가 연속적으로 사용.
예제: DGEMM 연산 (행렬 곱셈)
DGEMM의 루프는 다음과 같다:
for (int j = 0; j < n; ++j) {
for (int i = 0; i < n; ++i) {
C[i + j * n] = C[i + j * n];
for (int k = 0; k < n; ++k) {
C[i + j * n] += A[i + k * n] * B[k + j * n];
}
}
}이 코드는:
1. 행렬 A와 B에서 데이터를 읽음.
2. 행렬 C에 데이터를 저장.
문제:
• 행렬 크기가 크면 캐시 용량 초과로 인해 capacity misses(용량 미스)가 증가.
• 특정 데이터가 캐시에서 밀려난 후 재사용되어, 필요 이상의 메모리 액세스 발생.

4. 그림 5.20: Blocking이 없는 경우
캐시에서 한 번에 N-by-N 크기의 행렬 A, B, C를 모두 저장할 수 없다면:
• 각 행렬의 모든 데이터를 다시 읽어야 함.
• 최악의 경우, **2N^3 + N^2**번의 메모리 액세스 발생.
5. Blocking을 적용한 DGEMM
Blocking을 적용하면, 행렬 연산을 작은 BLOCKSIZE로 나눠 계산한다.
Blocking된 DGEMM은 다음과 같이 작성된다:
#define BLOCKSIZE 32
void do_block(int n, int si, int sj, int sk, double *A, double *B, double *C) {
for (int i = si; i < si + BLOCKSIZE; ++i)
for (int j = sj; j < sj + BLOCKSIZE; ++j) {
double cij = C[i + j * n];
for (int k = sk; k < sk + BLOCKSIZE; ++k) {
cij += A[i + k * n] * B[k + j * n];
}
C[i + j * n] = cij;
}
}
void dgemm(int n, double *A, double *B, double *C) {
for (int sj = 0; sj < n; sj += BLOCKSIZE)
for (int si = 0; si < n; si += BLOCKSIZE)
for (int sk = 0; sk < n; sk += BLOCKSIZE)
do_block(n, si, sj, sk, A, B, C);
}효과:
1. 각 블록의 데이터를 캐시에 적재한 후, 캐시가 밀리기 전에 최대한 많이 활용.
2. **용량 미스(capacity misses)**를 줄이고 캐시 효율성을 향상.

6. 그림 5.22: Blocking 후의 접근
BLOCKSIZE가 3인 경우:
• 이전보다 캐시 내에서 데이터를 재사용하는 빈도가 증가.
• 결과적으로 메모리 액세스가 줄어들어 성능이 향상됨.
7. Blocking이 성능에 미치는 영향
Blocking의 성능 개선은:
1. 캐시의 시간 지역성과 공간 지역성을 모두 활용.
2. 캐시 크기와 BLOCKSIZE에 따라 달라지며, 보통 2배에서 10배 이상의 성능 향상 가능.
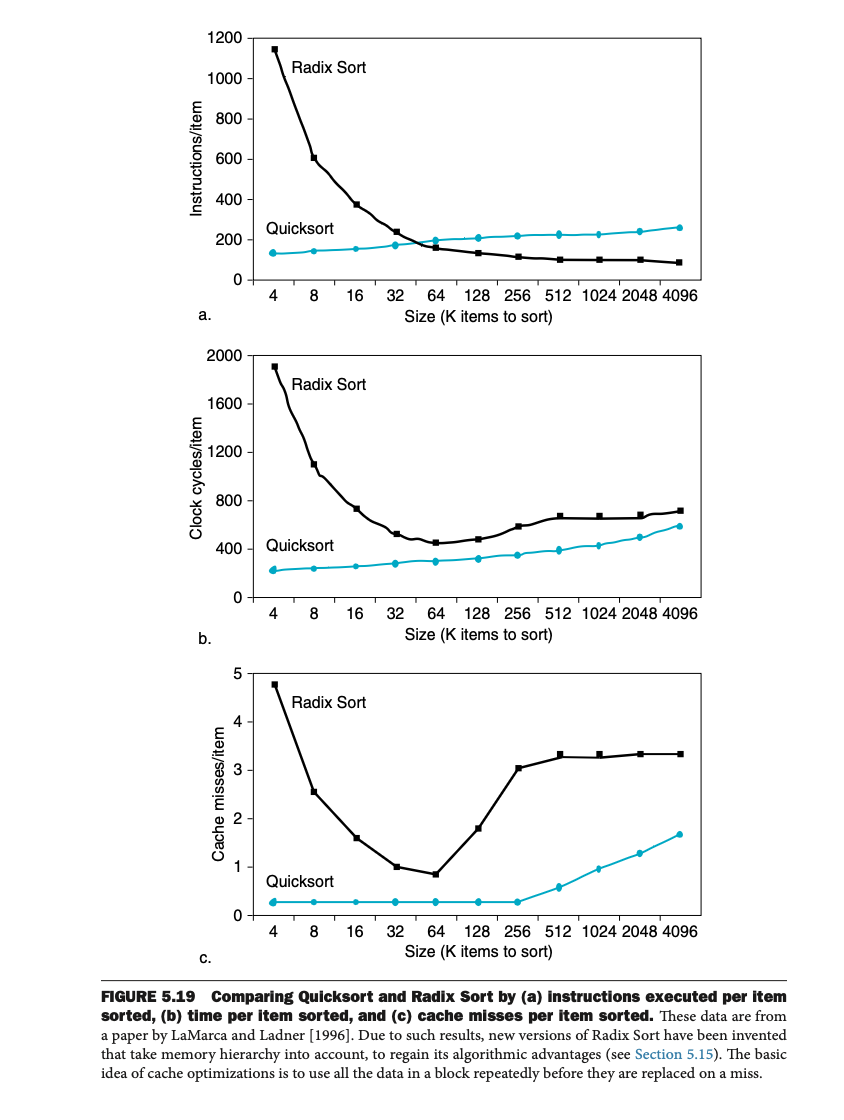
8. Quicksort와 Radix Sort의 캐시 성능 비교
그림 5.19는 Quicksort와 Radix Sort를 비교한 결과를 보여준다:
• a) Instructions per Item:
Radix Sort는 알고리즘적으로 더 많은 연산을 필요로 함.
• b) Clock Cycles per Item:
Radix Sort는 작은 데이터 크기에서는 비효율적이지만, 크기가 커질수록 Quicksort보다 효율적으로 작동.
• c) Cache Misses per Item:
Radix Sort는 더 많은 miss를 발생시켜 큰 데이터를 처리할수록 성능이 제한됨.
9. Blocking의 추가 이점
Blocking은 캐시 효율성 외에도 다음을 개선:
1. 레지스터 할당: 작은 BLOCKSIZE를 사용해 데이터를 레지스터에 유지.
2. Load/Store 감소: 필요하지 않은 메모리 연산 최소화.
10. 요약
• Blocking은 데이터의 지역성을 활용해 캐시 효율성을 극대화하는 기술.
• 배열과 행렬 연산에서 성능을 향상시키며, 일반적으로 메모리 액세스 비용을 줄임.
• Radix Sort와 같은 알고리즘은 캐시의 영향을 고려한 최적화가 필요.
• Blocking의 적절한 크기는 캐시 크기와 구조에 따라 다르며, 이를 조정하는 자동 튜닝(autotuning) 기법도 사용.
'Book > COMPUTER ORGANIZATION AND DESIGN RISC-V' 카테고리의 다른 글
| 5.6 Virtual Machines (0) | 2024.12.02 |
|---|---|
| 5.5 Dependable Memory Hierachy (0) | 2024.12.02 |
| 5.3 The Basics of Caches (0) | 2024.11.21 |
| 5.2 Memory Technologies (0) | 2024.11.20 |
| 5. Large and Fast: Exploiting Memory Hierarchy(5.1 Introduction) (0) | 2024.11.20 |