7.1 Computational Complexity
계산 복잡도란?
• **계산 복잡도(Computational Complexity)**는 특정 문제를 해결할 수 있는 모든 가능한 알고리즘의 효율성을 분석하는 학문이다.
• 주로 다음 두 가지를 분석한다:
1. 시간 복잡도(Time Complexity): 알고리즘이 실행되는 데 필요한 시간.
2. 공간 복잡도(Space Complexity): 알고리즘이 사용하는 메모리 양.
여기서 중요한 것은 알고리즘을 개별적으로 분석하는 것이 아니라 문제 자체의 본질적인 복잡도를 분석한다는 점이다.
예를 들어, 행렬 곱셈 문제에서는 최선의 알고리즘이라도 Θ(n²) 이상의 시간 복잡도를 가지며,
이를 문제의 **하한(Lower Bound)**이라고 한다.
정렬 문제의 계산 복잡도
정렬 문제를 계산 복잡도의 사례로 선택한 이유는 다음과 같다:
1. 이미 여러 정렬 알고리즘(예: 삽입 정렬, 선택 정렬, 합병 정렬 등)이 개발되어 있다.
2. 이 알고리즘들을 비교 분석하면 각 알고리즘의 강점과 약점을 이해할 수 있다.
3. 특정 클래스의 알고리즘에서 정렬 문제의 시간 복잡도는 **Ω(n log n)**이라는 하한이 증명되어 있다.
7.2 Insertion Sort and Selection Sort
Insertion Sort (삽입 정렬)
삽입 정렬은 이미 정렬된 배열에 새로운 원소를 올바른 위치에 삽입하는 방식으로 작동하는 정렬 알고리즘이다.
과정
1. 배열의 두 번째 원소부터 시작한다.
2. 현재 원소를 그보다 앞에 있는 원소들과 비교하여 올바른 위치에 삽입한다.
3. 이 과정을 배열 끝까지 반복한다.
예제
아래의 배열을 삽입 정렬로 정렬한다고 가정한다:
• 초기 배열: [4, 2, 7, 8, 9, 5, 1, 3]
과정:
• Step 1: 2를 4 앞에 삽입 → [2, 4, 7, 8, 9, 5, 1, 3]
• Step 2: 7은 이미 제자리에 있음 → [2, 4, 7, 8, 9, 5, 1, 3]
• Step 3: 8도 제자리에 있음 → [2, 4, 7, 8, 9, 5, 1, 3]
• Step 4: 9도 제자리에 있음 → [2, 4, 7, 8, 9, 5, 1, 3]
• Step 5: 5를 적절한 위치(4와 7 사이)에 삽입 → [2, 4, 5, 7, 8, 9, 1, 3]
• Step 6: 1을 적절한 위치에 삽입 → [1, 2, 4, 5, 7, 8, 9, 3]
• Step 7: 3을 적절한 위치에 삽입 → [1, 2, 3, 4, 5, 7, 8, 9]
Pseudo-Code
void insertionSort(int n, keytype S[]) {
index i, j;
keytype x;
for (i = 2; i <= n; i++) {
x = S[i];
j = i - 1;
while (j > 0 && S[j] > x) {
S[j + 1] = S[j];
j--;
}
S[j + 1] = x;
}
}
시간 복잡도
1. 최악의 경우(Worst Case): 입력 배열이 내림차순으로 정렬되어 있는 경우, 모든 원소를 비교해야 하므로 O(n²).
2. 평균적인 경우(Average Case): 각 원소가 랜덤하게 배치된 경우, 평균적으로 O(n²).
3. 최선의 경우(Best Case): 입력 배열이 이미 정렬된 경우, 비교만 수행하므로 O(n).
공간 복잡도
• 삽입 정렬은 제자리 정렬(In-place Sort) 알고리즘으로, 추가적인 메모리를 거의 사용하지 않는다.
• 공간 복잡도: Θ(1).
Selection Sort (선택 정렬)
선택 정렬은 배열에서 가장 작은 값을 선택하여 배열의 맨 앞자리로 옮기는 방식으로 작동한다.
과정
1. 배열에서 가장 작은 값을 찾아 첫 번째 원소와 교환한다.
2. 두 번째로 작은 값을 찾아 두 번째 원소와 교환한다.
3. 이 과정을 배열 끝까지 반복한다.
Pseudo-Code
void selectionSort(int n, keytype S[]) {
index i, j, smallest;
for (i = 1; i <= n - 1; i++) {
smallest = i;
for (j = i + 1; j <= n; j++) {
if (S[j] < S[smallest]) {
smallest = j;
}
}
exchange(S[i], S[smallest]);
}
}
시간 복잡도
• 모든 경우에서 O(n²). (비교 연산은 항상 동일한 수만큼 발생)
• 선택 정렬은 항상 배열을 끝까지 스캔해야 하므로 최선의 경우도 존재하지 않는다.
공간 복잡도
• 제자리 정렬(In-place Sort) 알고리즘으로 추가 메모리를 거의 사용하지 않음.
• 공간 복잡도: Θ(1).
삽입 정렬과의 비교
• 삽입 정렬은 평균적인 경우에서 선택 정렬보다 성능이 좋다.
• 선택 정렬은 교환 횟수가 적어 큰 레코드 배열에서 유리하다.
표(Table 7.1): Exchange, Insertion, Selection Sort 비교
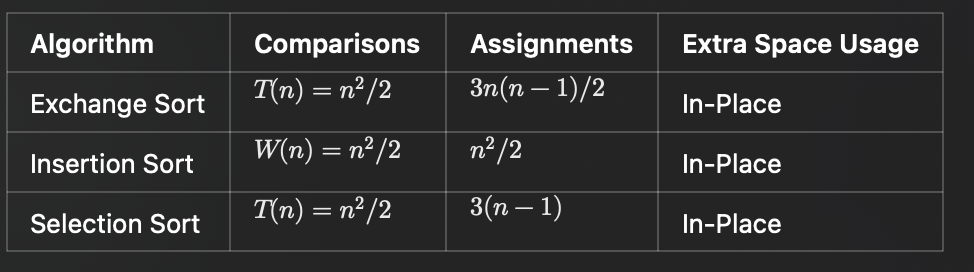
7.3 Lower Bounds for Algorithms that Remove at Most One Inversion per Comparison
Inversion이란?
• Inversion은 두 값 k_i와 k_j의 순서가 정렬된 배열과 다를 때를 의미한다. 즉, i < j인데도 k_i > k_j인 경우이다.
• 예: 배열 [3, 2, 4, 1, 6, 5]에서 다음과 같은 inversion이 존재:
• (3, 2), (3, 1), (2, 1), (4, 1), (6, 5).
• 총 5개의 inversion이 있다.
정렬 문제와 Inversion의 관계
정렬이란 결국 배열의 모든 inversion을 제거하는 과정이다.
• 정렬된 배열은 inversion이 없는 상태이다.
• 배열의 inversion을 한 번에 하나씩 제거할 수 있는 알고리즘(예: 삽입 정렬)은 최소 n(n-1)/2번의 비교를 해야 한다.
Theorem 7.1: 하한 정리
키 비교에만 의존하며, 각 비교 후 하나의 inversion만 제거할 수 있는 알고리즘은 다음이 성립한다:
• 최악의 경우(Worst Case): 최소 n(n-1)/2번의 비교가 필요하다.
• 평균적인 경우(Average Case): 최소 n(n-1)/4번의 비교가 필요하다.
증명 요약
1. 최악의 경우:
• 배열이 역순(예: [n, n-1, …, 2, 1])이라면 n(n-1)/2개의 inversion이 존재한다.
• 하나의 비교로 한 번에 하나의 inversion만 제거할 수 있으므로 최소 n(n-1)/2번의 비교가 필요하다.
2. 평균적인 경우:
• 배열의 모든 가능한 순열을 고려한다.
• 순열의 개수는 n!이며, 각 순열은 평균적으로 n(n-1)/4개의 inversion을 포함한다.
• 따라서 평균적으로 n(n-1)/4번의 비교가 필요하다.
7.4 Mergesort Revisited
**합병 정렬(Mergesort)**을 다시 분석하며, 왜 이 알고리즘이 Θ(n log n) 시간 복잡도를 가지는지 살펴본다.
합병 정렬의 개념
1. 배열을 반으로 나눈다(재귀적으로 반복).
2. 나뉜 배열을 정렬된 상태로 병합한다(merge).
3. 병합 과정에서 한 번의 비교로 여러 inversion을 제거할 수 있다.
인버전 제거의 효과
• Mergesort는 병합 단계에서 한 번의 비교로 여러 inversion을 제거할 수 있다.
• 예를 들어, 배열 [4, 3, 2, 1]을 합병 정렬로 정렬하는 과정에서:
1. 하위 배열 [4, 3]과 [2, 1]을 각각 정렬: [3, 4], [1, 2].
2. 병합 단계에서 [3, 4]와 [1, 2]를 비교하며 한 번에 (3, 1), (3, 2), (4, 1), (4, 2)의 inversion을 제거.
시간 복잡도 분석
1. 병합 단계: 두 배열의 크기가 n/2일 때, 병합에 걸리는 시간은 Θ(n)이다.
2. 재귀 단계: 전체 배열의 크기를 n에서 n/2, n/4, …, 1까지 줄인다. 이는 총 log n단계이다.
3. 전체 시간: 병합 단계 Θ(n) × 단계 수 Θ(log n) = Θ(n log n).
수식 분석
• 최악의 경우 병합 단계에서 필요한 비교 횟수:
W(n) = n * log n - (n-1)
여기서 W(n) ∊ Θ(n log n)임을 알 수 있다.
• 평균적인 경우 A(n)도 𝜭(n log n)임을 증명할 수 있다.
공간 복잡도 분석
• 합병 단계에서는 추가적인 배열이 필요하므로, 공간 복잡도는 **Θ(n)**이다.
• 개선된 Mergesort에서는 연결 리스트를 사용해 공간 복잡도를 줄일 수 있다(7.4에서 언급).
7.5 Quicksort Revisited
퀵 정렬 알고리즘
퀵 정렬은 분할 정복(Divide and Conquer) 방식의 대표적인 정렬 알고리즘이다.
배열을 재귀적으로 분할하고 병합하지 않고도 정렬을 수행하는 것이 특징이다.
Quicksort 코드
void quicksort(index low, index high) {
index pivotpoint;
if (high > low) {
partition(low, high, pivotpoint); // 분할 수행
quicksort(low, pivotpoint - 1); // 왼쪽 부분 배열 정렬
quicksort(pivotpoint + 1, high); // 오른쪽 부분 배열 정렬
}
}코드 설명
1. low와 high: 정렬할 배열의 범위를 나타낸다. 초기 호출 시 전체 배열의 시작과 끝을 나타낸다.
2. partition(low, high, pivotpoint):
• 배열을 피벗(Pivot) 기준으로 두 부분으로 나눈다.
• 피벗보다 작은 값은 왼쪽에, 큰 값은 오른쪽에 배치한다.
• 최종적으로 피벗의 위치(pivotpoint)를 반환한다.
3. 재귀 호출:
• low부터 pivotpoint-1까지의 하위 배열을 정렬.
• pivotpoint+1부터 high까지의 하위 배열을 정렬.
4. 종료 조건: low >= high일 때(정렬할 부분 배열이 없을 때) 종료.
퀵 정렬의 성능 분석
최악의 경우 (Worst Case)
• 배열이 이미 정렬되어 있는 경우, 피벗이 항상 배열의 가장 작은 값이나 가장 큰 값으로 선택되면, 한쪽 하위 배열만 생성된다.
• 이 경우 재귀 깊이가 n-1에 도달하며, 총 비교 횟수는 다음과 같다:
T(n) = T(n-1) + n
이를 풀면 O(n^2)이 된다.
평균적인 경우 (Average Case)
• 피벗이 배열을 균등하게 나누는 경우, log n 단계가 발생하며, 각 단계에서 배열의 모든 요소를 한 번씩 비교한다.
• 이 경우 총 비교 횟수는 다음과 같다:
A(n) = 1.38(n+1) log n
따라서 **평균 시간 복잡도는 𝜭(n log n)**이다.
공간 복잡도
• 퀵 정렬은 제자리 정렬(In-place Sort) 알고리즘이지만, 재귀 호출로 인해 스택 공간을 사용한다.
• 최악의 경우 스택 깊이는 O(n), 평균적인 경우 O(log n)이다.
퀵 정렬과 Mergesort 비교
1. 시간 복잡도:
• Mergesort: 항상 𝜭(n log n).
• Quicksort: 평균 𝜭(n log n), 최악 O(n^2).
2. 공간 복잡도:
• Mergesort: 추가 배열 사용(공간 복잡도 O(n)).
• Quicksort: 제자리 정렬(공간 복잡도 O(log n) 스택 사용).
3. 실제 성능:
• 평균적인 경우, 퀵 정렬은 Mergesort보다 빠르다.
이는 데이터가 메모리에 저장된 방식과 퀵 정렬의 캐시 친화성(Cache Friendliness) 때문이다.
퀵 정렬의 개선 방법
퀵 정렬의 단점을 보완하기 위해 몇 가지 개선 방법이 제시되었다.
1. 재귀 호출의 최적화
• 재귀 호출로 인해 발생하는 스택 사용량을 줄이기 위해, 큰 하위 배열만 재귀 호출하고 작은 하위 배열은 반복문을 사용한다.
• 이를 통해 스택 깊이를 줄여 공간 복잡도를 Θ(log n)로 제한할 수 있다.
2. 피벗 선택 전략 변경
• 단순히 첫 번째 원소나 마지막 원소를 피벗으로 선택하지 않고, 중간값(Median-of-Three) 전략을 사용한다.
• 피벗 후보 3개를 선택: S[low], S[(low + high)/2], S[high].
• 이 중 중간값을 피벗으로 사용.
• 중간값 전략은 배열이 정렬된 경우에도 한쪽으로 치우치지 않도록 하여 최악의 경우를 피할 가능성을 높인다.
3. 하위 배열 크기 임계값 설정
• 배열 크기가 작아지면, 퀵 정렬 대신 삽입 정렬(Insertion Sort)을 사용한다.
• 작은 배열에서는 삽입 정렬이 오버헤드가 적고 더 효율적이다.
4. 비재귀적인 구현
• 명시적으로 스택을 사용하여 재귀를 제거하고 반복문 기반의 퀵 정렬을 구현할 수 있다.
• 이를 통해 호출 스택의 오버헤드를 줄인다.
7.6 힙 정렬(Heapsort)
힙 정렬의 주요 단계
1. 힙 구조와 기본 연산
1. 힙의 정의:
• 힙은 완전 이진 트리로 구성되며, 힙 속성을 만족한다.
• 최대 힙(Max-Heap): 부모 노드 값 ≥ 자식 노드 값.
• 최소 힙(Min-Heap): 부모 노드 값 ≤ 자식 노드 값.
2. 완전 이진 트리 배열 표현:
• 배열에서 루트 노드는 인덱스 1에 저장된다.
• 노드 i의:
• 왼쪽 자식: 2i
• 오른쪽 자식: 2i + 1
• 부모: ⌊i / 2⌋
2. makeheap 단계
힙 정렬의 첫 번째 단계는 배열을 **최대 힙(Max-Heap)**으로 변환하는 것이다. 이를 위해 siftdown 연산을 반복적으로 호출한다.
• makeheap의 동작:
1. 힙의 마지막 내부 노드(⌊n / 2⌋)부터 시작하여 루트 노드까지 **siftdown**을 수행.
2. 각 노드에서 아래로 내려가며 힙 속성을 만족하도록 조정.
• 시간 복잡도 분석:
• 힙의 높이 d = ⌊log n⌋.
• 각 노드에서 siftdown 호출은 최대 O(log n) 시간이 소요된다.
• 깊이별 노드 개수와 이동하는 횟수 합산:
• 깊이 j에서 노드 개수: 2^j
• 각 노드에서 d - j번 이동.
• 총 비용:

• 결론: 힙을 생성하는 시간은 **O(n)**이다.
3. 정렬 단계
makeheap 이후에는 최대 힙에서 반복적으로 루트 노드(최댓값)를 제거하고 배열 뒤로 이동시키며 정렬을 수행한다.
• 단계 설명:
1. 루트 노드(최대값)를 배열의 끝과 교환.
2. 힙 크기를 줄이고, 교환된 루트 값에 대해 siftdown 수행.
3. 이를 반복하여 정렬 완료.
• 시간 복잡도 분석:
• 루트 노드 제거 및 교환: O(1).
• 힙 복구(siftdown): O(log n).
• 총 반복 횟수: n - 1.
• 결론: 정렬 단계의 시간 복잡도는 **O(n log n)**이다.
시간 복잡도 분석
1. siftdown 분석
• 최악의 경우:
• 루트에서 리프까지 내려가야 하므로 호출당 O(log n).
• 전체 호출 횟수:
• 힙 생성(makeheap) 중에는 노드 개수에 따라 적은 횟수만 이동.
• 정렬 중에는 총 n-1번 호출.
• 결과적으로 정렬 단계는 O(n log n).
2. makeheap 분석
• 앞서 설명했듯이, 힙 생성은 **O(n)**이다.
3. 전체 시간 복잡도
• 힙 생성: O(n).
• 정렬: O(n log n).
• 결론: 전체 힙 정렬의 시간 복잡도는 O(n log n).
공간 복잡도 분석
힙 정렬은 in-place 알고리즘이다. 입력 배열을 재활용하며 추가 메모리는 최소화된다.
• 추가 공간:
• 배열 외에 사용되는 추가 변수는 고정 크기(O(1)).
• 결론: 공간 복잡도는 **O(1)**이다.
코드 상세 설명
1. siftdown 함수
siftdown은 특정 노드에서부터 힙 속성을 복구하는 함수이다.
void siftdown(heap& H, index i) {
index parent, largerchild;
keytype siftkey;
bool spotfound = false;
siftkey = H.S[i]; // 현재 노드 값 저장
parent = i;
while ((2 * parent <= H.heapsize) && !spotfound) {
// 자식 중 더 큰 값을 가진 노드 선택
if (2 * parent < H.heapsize && H.S[2 * parent] < H.S[2 * parent + 1])
largerchild = 2 * parent + 1;
else
largerchild = 2 * parent;
if (siftkey < H.S[largerchild]) {
H.S[parent] = H.S[largerchild];
parent = largerchild;
} else
spotfound = true;
}
H.S[parent] = siftkey;
}• 핵심 동작:
• 현재 노드 값을 저장하고 자식 노드와 비교.
• 부모-자식 간의 교환 반복.
2. makeheap 함수
배열을 최대 힙으로 변환하는 함수이다.
void makeheap(int n, heap& H) {
H.heapsize = n;
for (int i = n / 2; i >= 1; i--)
siftdown(H, i);
}• 동작 원리:
• 마지막 내부 노드부터 루트까지 역순으로 siftdown 수행.
• 힙 구조를 유지하며 배열 변환.
3. heapsort 함수
전체 힙 정렬 과정을 수행하는 함수이다.
void heapsort(int n, heap& H) {
makeheap(n, H);
for (int i = n; i >= 2; i--) {
std::swap(H.S[1], H.S[i]);
H.heapsize--;
siftdown(H, 1);
}
}• 핵심 과정:
1. 배열을 최대 힙으로 변환.
2. 루트 값을 배열 뒤로 이동시키고, 힙 복구.
3. 이를 반복하여 정렬.
Heapsort의 분석 요약
1. 시간 복잡도:
• 최악, 평균, 최선: O(n log n).
2. 공간 복잡도:
• O(1) (제자리 정렬).
3. 특징:
• 안정적이지 않다(Stable Sort 아님).
• 메모리 효율적.
7.7 Comparison of Mergesort, Quicksort, and Heapsort
세 알고리즘에 대한 비교는 앞서 다룬 내용에서 크게 변하지 않는다.
1. Heapsort
• 특징:
• 힙 자료구조를 기반으로 정렬한다.
• 시간 복잡도는 항상 O(n log n) 이다.
• In-place 정렬이기 때문에 추가 메모리 사용량은 O(1) 이다.
• 한계:
• 키 비교와 데이터 이동이 많아 평균적으로 Quicksort보다 느리다.
• 힙 구조에서 데이터를 빼내면서 발생하는 상수 계수가 크다.
• 요약: 메모리 효율은 좋지만 실제 성능은 Quicksort보다 떨어질 수 있다.
2. Mergesort
• 특징:
• 데이터를 반복적으로 두 부분으로 나눠 정렬하고 병합한다.
• 시간 복잡도는 O(n log n) 로 Heapsort와 같다.
• 한계:
• 추가 메모리 공간이 필요하다 ( O(n) ).
• 병합 과정에서 메모리 이동이 많아 상수 계수가 크다.
• 요약: 안정적이고 일정한 성능을 보장하지만, 메모리 사용량이 단점이다.
3. Quicksort
• 특징:
• 피벗(pivot)을 선택해 배열을 두 그룹으로 나누고 정렬을 반복한다.
• 평균 시간 복잡도는 O(n \log n) , 최악의 경우 O(n^2) 이다.
• 한계:
• 최악의 경우 O(n^2) 이 발생하지만, 일반적으로 피벗 선택 방식을 개선해 이를 회피한다.
• 요약: 메모리와 성능 면에서 균형이 잘 잡혀 있어 실제로 가장 선호된다.
Table 7.2 분석

• 깊이(depth): 트리 구조의 높이를 나타낸다.
• 노드 개수: 깊이별로 키가 이동하는 최대 노드 개수를 나타낸다.
• 이 표는 키 이동 횟수가 어떻게 \log n 에 비례하는지를 보여주는 도구로 사용된다.
7.8 Lower Bounds for Sorting Only by Comparison of Keys
이 섹션은 “키 비교만으로 정렬하는 알고리즘의 시간 복잡도는 O(n \log n) 보다 낮아질 수 없는 이유”를 설명한다.
핵심은 **Decision Tree(결정 트리)**와 수학적 증명을 통해 이 하한선을 보이는 것이다.
7.8.1 Decision Trees for Sorting Algorithms
1. 코드 분석 (sortthree)
void sortthree(keytype S[]) {
keytype a, b, c;
a = S[1]; b = S[2]; c = S[3];
if (a < b)
if (a < c)
if (b < c)
S = {a, b, c};
else
S = {a, c, b};
else
S = {c, a, b};
else
if (b < c)
if (a < c)
S = {b, a, c};
else
S = {b, c, a};
else
S = {c, b, a};
}• 이 코드는 세 개의 키 a, b, c 를 정렬한다.
• 비교 횟수:
• 최대 3번의 비교를 통해 6가지 순열 중 하나를 고를 수 있다.
• 각 비교 결과는 결정 트리의 **가지(branch)**로 나타난다.
2. 결정 트리의 구성
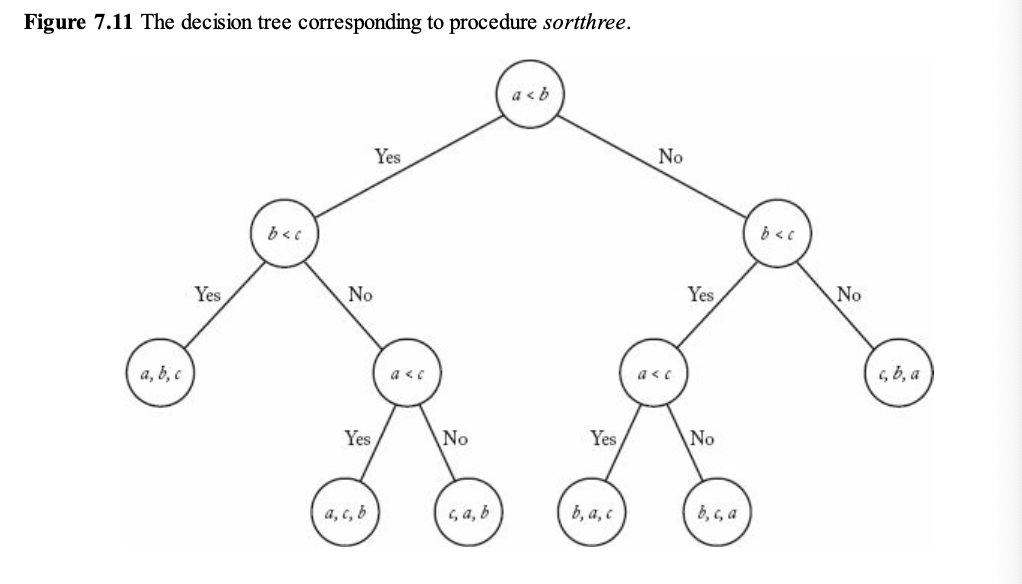
• Figure 7.11은 sortthree 코드의 결정 트리를 나타낸다.
• 각 노드는 두 키를 비교하는 연산을 나타낸다.
• 각 리프 노드는 정렬된 결과(예: \{a, b, c\} )를 나타낸다.
Lemma 7.1 설명
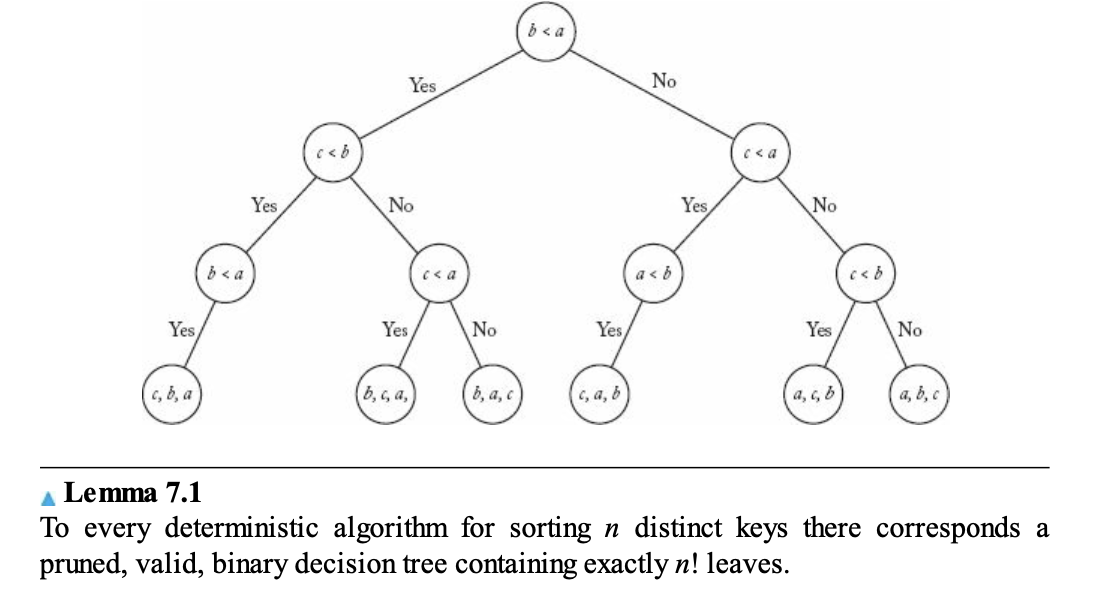
• 결정 트리란, 모든 가능한 입력 순열에 대해 정확히 하나의 리프를 가지는 트리이다.
• n 개의 키를 정렬하는 알고리즘은 반드시 n! 개의 리프를 가진다. n! 은 가능한 모든 입력의 정렬 결과를 나타낸다.
• 이 트리는 각 경로가 고유해야 하므로, n! 개의 리프를 가지려면 깊이가 최소 \log(n!) 가 되어야 한다.
7.8.2 Lower Bounds for Worst-Case Behavior
Lemma 7.2
• 트리의 깊이는 최악의 경우 비교 횟수를 나타낸다.
• 즉, 최악의 경우 비교 횟수는 트리에서 가장 긴 경로의 길이와 같다.
Lemma 7.3
• 트리에 n! 개의 리프가 필요하므로, 깊이는 \log(n!) 이상이어야 한다.
Theorem 7.2 증명
1. n! 은 n 개의 입력의 가능한 모든 순열의 개수이다.
2. n! 개의 리프를 가지는 트리의 깊이는 최소 [\log(n!)] 이다.
3. Stirling’s Approximation을 사용하면 \log(n!) ≈ n \log n - n 이므로, [n \log n - n ] 이 최악의 비교 횟수가 된다.
7.8.3 Lower Bounds for Average-Case Behavior
평균적인 경우에도 유사한 하한선을 계산할 수 있다.
Lemma 7.5
• 모든 결정 트리는 2-트리로 변환 가능하며, 이는 최소한 기존 트리만큼 효율적이다.
• 2-트리란? 모든 내부 노드가 정확히 두 자식을 가지는 이진 트리이다.
Theorem 7.4
• 평균 비교 횟수는 n \log n - 1.45n 이상이다.
• 이 하한선은 실제 정렬 알고리즘(Mergesort, Quicksort 등)의 평균 성능과 거의 일치한다.
7.9 Sorting by Distribution (Radix Sort)
Radix Sort란?
Radix Sort는 정렬할 데이터가 **자릿값(기수, radix)**으로 구성된 경우에 자릿값을 활용해 정렬하는 알고리즘이다.
이 알고리즘은 다음의 기본 원칙을 따른다:
1. 입력 값이 자릿값들로 이루어져 있다는 것을 전제로 한다.
예를 들어, 10진수로 이루어진 숫자가 있다면 각 자릿수(일의 자리, 십의 자리 등)를 기준으로 정렬한다.
2. 자릿값을 하나씩 차례로 확인하며 데이터를 정렬해 나간다. 가장 낮은 자릿수부터 높은 자릿수까지 진행하거나 그 반대로 할 수 있다.
작동 원리
1. 숫자를 자릿수 별로 그룹화
• 가장 오른쪽 자릿수(일의 자리)부터 시작하여 각 숫자를 해당 자릿값에 따라 그룹으로 나눈다.
• 예를 들어, 숫자 416, 317, 123이 있다면 일의 자리를 기준으로 416(6), 317(7), 123(3)을 분류한다.
2. 다음 자릿수로 진행
• 그룹화한 데이터를 다시 병합한 뒤, 다음 자릿수를 기준으로 그룹화한다. 이 과정을 가장 왼쪽 자릿수까지 반복한다.
3. 완전한 정렬
• 모든 자릿수에 대해 그룹화를 마치면 데이터는 정렬되어 있다.
Figure 7.14와 Figure 7.15
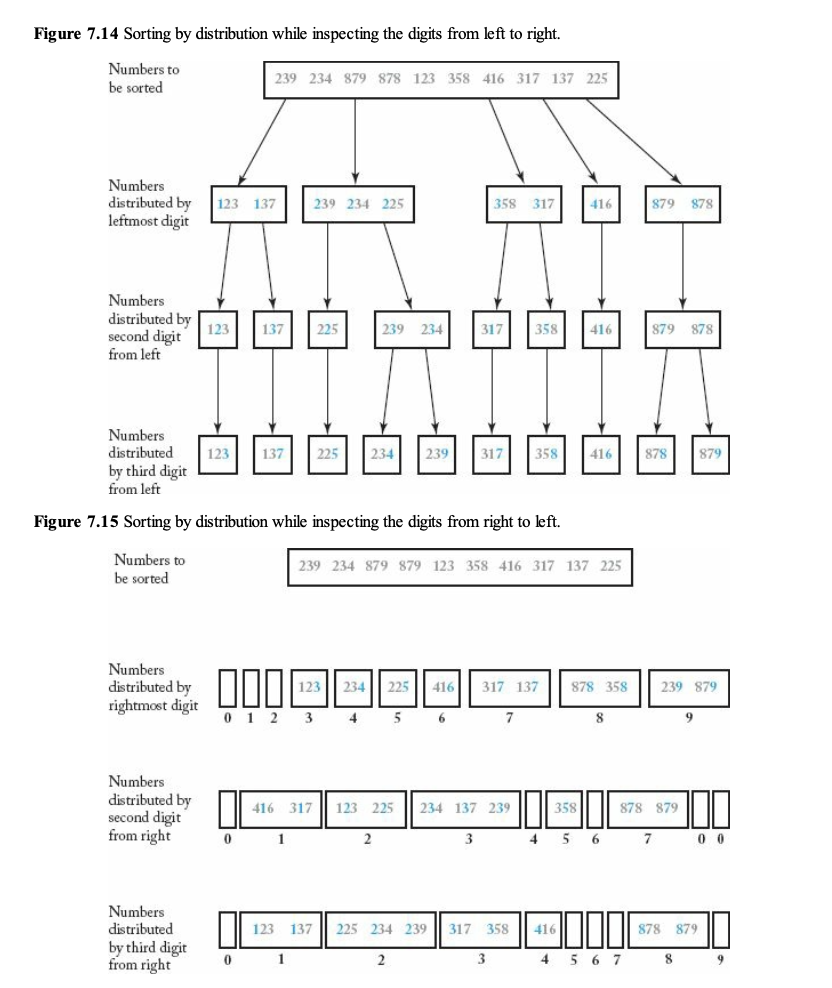
• Figure 7.14는 숫자를 왼쪽에서 오른쪽으로 정렬하는 과정을 보여준다.
• Figure 7.15는 숫자를 오른쪽에서 왼쪽으로 정렬하는 과정을 보여준다.
• 예를 들어, 416과 317을 살펴보면:
• 첫 번째(오른쪽) 자릿수 정렬 후: 416(6), 317(7).
• 두 번째(가운데) 자릿수 정렬 후: 416(1), 317(1).
• 세 번째(왼쪽) 자릿수 정렬 후: 최종적으로 정렬된다.
구현 (Algorithm 7.6)
Radix Sort는 자릿수를 하나씩 검사하며 데이터를 **분배(distribute)**하고 다시 **병합(coalesce)**하는 방식으로 작동한다.
자료구조
• struct nodetype:
• 데이터를 저장하는 연결 리스트를 표현한다.
• 각 숫자는 자릿값에 따라 서로 다른 “리스트”에 저장된다.
struct nodetype {
keytype key; // 저장할 값
nodetype* link; // 다음 노드를 가리키는 포인터
};
typedef nodetype* node_pointer;
1. Main Function (radixsort)
void radixsort(node_pointer& masterlist, int numdigits) {
node_pointer list[0..9]; // 10개의 리스트(0부터 9까지의 자릿값)
for (int i = 1; i <= numdigits; i++) {
distribute(masterlist, i); // 자릿값에 따라 분배
coalesce(masterlist); // 병합하여 다시 정렬
}
}• numdigits: 정렬할 데이터의 최대 자릿수.
• 분배와 병합을 반복하여 데이터를 정렬한다.
2. Distribute (자릿값 분배)
void distribute(node_pointer& masterlist, index i) {
node_pointer p = masterlist; // 현재 리스트의 시작점
while (p != NULL) {
int j = value of ith digit in p->key; // i번째 자릿값 추출
link p to the end of list[j]; // 해당 자릿값에 따라 노드를 리스트에 추가
p = p->link;
}
}• 현재 자릿값을 기준으로 데이터를 각각의 리스트(0~9)에 분배한다.
• n 개의 데이터를 분배하기 때문에 분배 과정의 시간 복잡도는 O(n) 이다.
3. Coalesce (병합)
void coalesce(node_pointer& masterlist) {
masterlist = NULL;
for (int j = 0; j <= 9; j++) {
link the nodes in list[j] to the end of masterlist;
}
}• 모든 리스트(0~9)의 데이터를 하나의 리스트로 병합한다.
• 이 과정의 시간 복잡도도 O(n) 이다.
시간 복잡도 분석
Radix Sort의 시간 복잡도를 T({numdigits}, n) 로 나타낼 수 있다:
1. 각 자릿값에 대해 분배와 병합을 수행하므로, 자릿값의 수 {numdigits} 와 데이터의 크기 n 에 비례한다.
2. 따라서:
T({numdigits}, n) = {numdigits} * (n + 10) ∊ 𝜭({numdigits} * n)
최악의 경우
• 만약 {numdigits} 가 데이터 크기 n 과 같다면, 시간 복잡도는 O(n^2) 이다.
실제 활용
• 일반적으로 자릿값의 개수는 n 보다 훨씬 작기 때문에 O(n \log n) 의 효율에 근접한다.
공간 복잡도 분석
Radix Sort의 추가 공간 사용은 다음과 같다:
1. 모든 리스트는 연결 리스트로 구현되며, 데이터 자체를 복사하지 않는다.
2. 따라서 O(n) 개의 추가 링크가 필요하다.
결론
Radix Sort는 다음과 같은 특징을 가진다:
• 시간 복잡도: O(n \log n) 에 근접.
• 공간 복잡도: O(n) .
Radix Sort의 한계
1. 데이터가 고정된 자릿값으로 구성되어 있어야 한다.
• 예: 정수나 특정 고정 길이의 문자열.
2. **기수(radix)**가 클수록 분배 과정이 복잡해진다.
장점
1. 키 비교를 하지 않는다는 점에서 O(n \log n) 정렬보다 효율적일 수 있다.
2. 특히, 자릿값이 적은 정렬에서 매우 효율적이다.
'Book > Foundations Of Algorithms' 카테고리의 다른 글
| CH8. More Computational Complexity: The Searching Problem (0) | 2024.12.10 |
|---|---|
| CH2_Exercise (0) | 2024.10.16 |
| CH1.Exercise (1) | 2024.10.14 |