1. Write an algorithm that finds the largest number in a list (an array) of n numbers.
int fintLargest(std::vector<int>& v){
int largest = v[0];
for(int i=1; i<v.size(); i++){
if(v[i] > largest) largest = v[i];
}
}
2. Write an algorithm that finds the m smallest numbers in a list of n numbers.
std::vector<int> findSmallThanM(std::vector<int>& v, int m){
std::sort(v.begin(), v,end());
std::vector<int> result(v.begin(), v.begin()+m);
return result;
}
3. Write an algorithm that prints out all the subsets of three elements of a set of n elements. The elements of this set are stored in a list that is the input to the algorithm.
void PrintSubsetOfThree(std::vector<int>& v) {
int n = v.size();
for (int i = 0; i < n - 2; i++) {
for (int j = i + 1; j < n - 1; j++) {
for (int k = j + 1; k < n; k++) {
std::cout << v[i] << "," << v[j] << "," << v[k] << '\n';
}
}
}
}
4. Write an Insertion Sort algorithm (Insertion Sort is discussed in Section 7.2) that uses Binary Search to find the position where the next insertion should take place.
int binarySearch(std::vector<int>& v, int item, int low, int high) {
while (low <= high) {
int mid = low + (high - low) / 2;
if (v[mid] == item)
return mid + 1;
else if (v[mid] < item)
low = mid + 1;
else
high = mid - 1;
}
return low;
}
void insertionSort(std::vector<int>& v) {
int n = v.size();
for (int i = 1; i < n; i++) {
int key = v[i];
int j = i - 1;
int loc = binarySearch(v, key, 0, j);
while (j >= loc) {
v[j + 1] = v[j];
j--;
}
v[j + 1] = key;
}
}
5. Write an algorithm that finds the greatest common divisor of two integers.
int gcd(int a, int b) {
if (b == 0) return a;
return gcd(b, a % b);
}
6. Write an algorithm that finds both the smallest and largest numbers in a list of n numbers. Try to find a method that does at most 1.5n comparisons of array items
std::pair<int, int> findMinMax(const std::vector<int>& arr) {
int n = arr.size();
int minVal, maxVal;
if (n % 2 == 0) {
minVal = std::min(arr[0], arr[1]);
maxVal = std::max(arr[0], arr[1]);
} else {
minVal = maxVal = arr[0];
}
for (int i = (n % 2 == 0) ? 2 : 1; i < n; i += 2) {
int localMin = std::min(arr[i], arr[i + 1]);
int localMax = std::max(arr[i], arr[i + 1]);
minVal = std::min(minVal, localMin);
maxVal = std::max(maxVal, localMax);
}
return {minVal, maxVal};
}
7. Write an algorithm that determines whether or not an almost complete binary tree is a heap.
bool isHeap(const std::vector<int>& arr) {
int n = arr.size();
for (int i = 0; i <= (n - 2) / 2; ++i) {
if (2 * i + 1 < n && arr[i] < arr[2 * i + 1]) return false;
if (2 * i + 2 < n && arr[i] < arr[2 * i + 2]) return false;
}
return true;
}
8. Under what circumstances, when a searching operation is needed, would Sequential Search (Algorithm 1.1) not be appropriate?
1
순차 탐색은 데이터의 수가 매우 많을 때 비효율적이다.
2
순차 탐색은 데이터가 정렬되어 있을 떄 비효율적이다
3
순차 탐색은 빠른 탐색을 해야할 때 비효율적이다
시간복잡도가 평균적으로 O(n)이므로 위의 상황일 떄는
평균 O(log n)인 이진탐색을 사용하는 것이 더 낫다.
9. Give a practical example in which you would not use Exchange Sort (Algorithm 1.3) to do a sorting task.
Exchange Sort = 버블정렬
시간 복잡도가 O(n^2) 이기 때문에
데이터의 규모가 클 때,
데이터가 이미 일정 부분 정렬되어 있을 떄(정렬되어 있어도 하나하나 확인함)
버블정렬은 적합하지 않다.
10. Define basic operations for your algorithms in Exercises 1–7, and study the performance of these algorithms. If a given algorithm has an every-case time complexity, determine it. Otherwise, determine the worst-case time complexity.
1. Finding the Largest Number in Array -> O(n)
//this algorithm has to compare all every elements in list.
//so its time complexity is O(n) in the worst case.
2. Finding the m Smallest Number in Array -> O(nlog n)
//this algorithm has to be sorted and then find num small than m.
//sort has O(nlong n) time complexity and find has O(m).
//so the time complexity is O(nlong n)
3. Printing all Subsets of Three Elements from the Array ->O(n^3)
//this algorithm has 3 for Loop.
//so the time complexity is O(n^3)
4. Insertion Sort using Binary Search -> O(n^2)
//binary search takes O(log n) but in insertion search,
//shifting elements still takes O(n).
//so the time complexity is O(n^2)
5. Finding GCD -> O(log min(a,b))
//using uclid algorithm that uses moduler operation repeatedly
//so the time complexity is O(log min(a,b))
6. Finding both the smallest and largest numbers in a Array -> O(n)
//this can be done in 1.5n comparisons in the worst case
//so the time complexity is O(n)
7. Determining whether a binary tree is a heap -> O(n)
//to check binary heap is a heap,
//we must check the parent node is bigger than child
//because every element except leaf must be checked,
//the time complexity is O(n)
11. Determine the worst-case, average-case, and best-case time complexities for the basic Insertion Sort and for the version given in Exercise 4, which uses Binary Search.
#Basic InsertionSort
//best case -> O(n)
when the array is already sorted, we don't have to move elements.
Each insertion is done in constant time
//average case -> O(n^2)
elements will be inserted in random order.
elements have to shifted to the position.
//worst case -> O(n^2)
when the array is sorted in reversed order,
every element must be shifted.
#InsertionSort Using BinarySearch
//best case -> O(log n)
it is same with Basic InsertionSort's best case.
but binarysearch takes O(log n) to find positions.
//average case -> O(n^2)
binary search can reduce time that finds position to O(log n)
but shifting elements still takes O(n)
//worst case -> O(n^2)
It is similar to average case
binary searching takes O(log n)
but shifting elements still takes O(n)
12. Write a Θ(n) algorithm that sorts n distinct integers, ranging in size between 1 and kn inclusive, where k is a constant positive integer. (Hint: Use a knelement array.)
#counting sort
#include <iostream>
#include <vector>
void countingSort(std::vector<int>& arr, int k) {
int n = arr.size();
int max_val = k * n; // Maximum possible value in the array
// Create a counting array of size kn + 1
std::vector<bool> count(max_val + 1, false);
// Mark the presence of each number in the counting array
for (int i = 0; i < n; ++i) {
count[arr[i]] = true;
}
// Output the sorted array by iterating through the counting array
int index = 0;
for (int i = 1; i <= max_val; ++i) {
if (count[i]) {
arr[index++] = i;
}
}
}
13. Algorithm A performs 10n2 basic operations, and algorithm B performs 300 ln n basic operations. For what value of n does algorithm B start to show its better performance?
계산힘들어서 pass
14. There are two algorithms called Alg1 and Alg2 for a problem of size n. Alg1 runs in n2 microseconds and Alg2 runs in 100n log n microseconds. Alg1 can be implemented using 4 hours of programmer time and needs 2 minutes of CPU time. On the other hand, Alg2 requires 15 hours of programmer time and 6 minutes of CPU time. If programmers are paid 20 dollars per hour and CPU time costs 50 dollars per minute, how many times must a problem instance of size 500 be solved using Alg2 in order to justify its development cost?
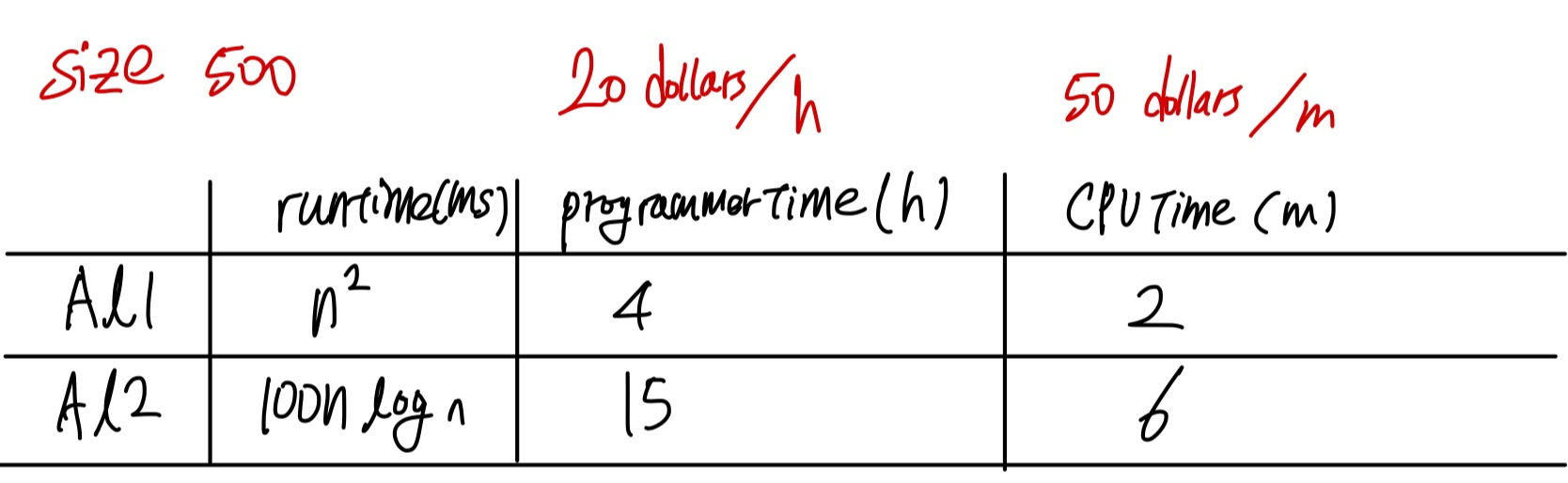
#cost
al1 -> 20*4 + 50*2 = 180
al2 -> 15*20 + 50*6 = 600
#running time
al1 -> 500^2 = 250000
al2 -> 100 * 500 * log(500) = 134948.5
15 Show directly that f(n) = n^2 + 3n^3 ∈ Θ(n3). That is, use the definitions of O and Ω to show that f(n) is in both O(n3) and Ω(n3).
#Big-O
f(n) = n^2 + 3n^3
the dominant term is 3n^3
f(n) <= c*n^3 for some constant c and sufficiently large n
#Big-Omega
f(n) = n^2 + 3n^3
the dominant term is 3n^3
f(n) >= c*n^3 for some constant c and sufficiently large n
Choose c = 4
then for n >= 1 , we have f(n) <= 4n^3 , proving f(n) is in O(n^3)
Choose c = 3
then for n >= 1 , we have f(n) >= 3n^3 , proving f(n) is in 𝜭(n^3)
#conclusion
Since f(n) is in O(n^3) and f(n) is in 𝜭(n^3),
if follows that f(n) is in 𝜭(n^3)
16. Using the definitions of O and Ω, show that 6n^2 + 20n is in O(n^3) but 6n^2 + 20n is not in Omega(n^3)
#Big-O
f(n) = 6n^2 + 20n
the dominant term is 6n^2
Since 6n^2 <= c*n^3,
f(n) is in O(n^3)
#Big-Omega
f(n) = 6n^2 + 20n
the dominant term is 6n^2
if c=1 and n is small number, f(n) >= n^3
Hence f(n) is not in 𝜴(n^3)
17. Using the Properties of Order in Section 1.4.2, show that
5n^5 + 4n^4 + 6n^3 + 2n^2 + n + 7 is in 𝜭(n^5)
the dominant term of f(n) is 5n^5
#Big-O
if c is sufficiently large number,
f(n)<=cn^5 for some constant c
#Big-Omega
if c is smaller than 5,
f(n)>=cn^5
Thus, f(n) is in 𝜭(n^5)
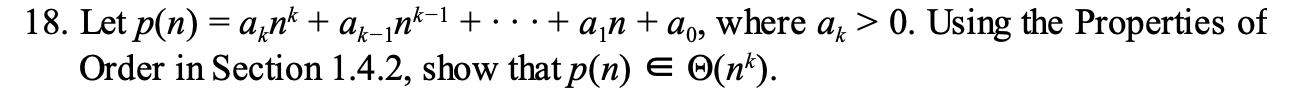
#Big-O
For large n,
p(n) <= cn^k
#Big-Omega
For large n,
p(n) >= cn^k
so
p(n) is in 𝜭(n^k)

ans : e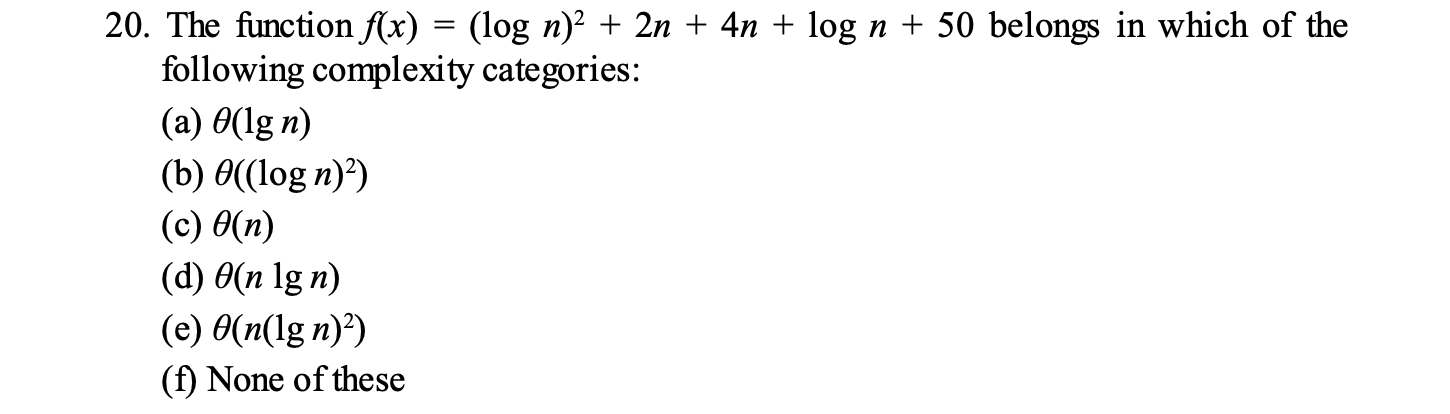
ans : c
ans : none of this
𝜭(2^n)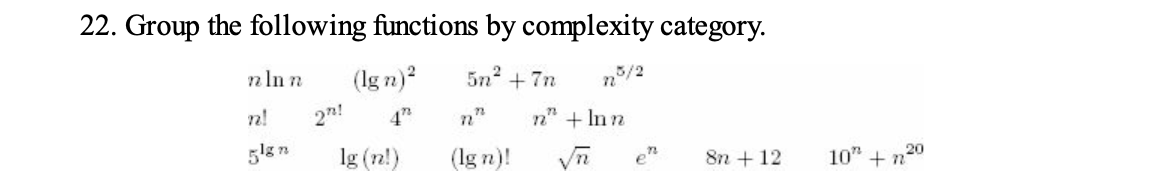
23. Establish Properties 1, 2, 6, and 7 of the Properties of Order in Section 1.4.2.
24. Discuss the reflexive, symmetric, and transitive properties for asymptotic comparisons (O, Ω, Θ, o).
Reflexive:
A function f(n) is reflexive because f(n) = O(f(n)) ,
f(n) = \Omega(f(n)) , and f(n) = \Theta(f(n)) .
Symmetric:
Big-O and Big-Omega are not symmetric, but Theta is symmetric.
If f(n) = O(g(n)) , it doesn’t imply g(n) = O(f(n)) ,
but if f(n) = \Theta(g(n)) , then g(n) = \Theta(f(n)) .
Transitive:
If f(n) = O(g(n)) and g(n) = O(h(n)) , then f(n) = O(h(n)) .
This also applies for \Omega and \Theta ,
meaning that the relationships between asymptotic notations are transitive.


26. Derive the proof of Theorem 1.3.


all true'Book > Foundations Of Algorithms' 카테고리의 다른 글
| CH8. More Computational Complexity: The Searching Problem (0) | 2024.12.10 |
|---|---|
| CH7. Introduction to Computational Complexity: The Sorting Problem (1) | 2024.12.05 |
| CH2_Exercise (1) | 2024.10.16 |