이번에는 퀵정렬에 대해 알아보겠습니다.
퀵정렬은 배열을 두 부분으로 나누고 다시 합치는 과정에서 병합 정렬과 비슷한 면이 있지만,
배열을 절반으로 자르는 병합 정렬과는 달리
퀵정렬은 pivot 값을 중심으로 배열을 두 개로 나눕니다.
이떄 pivot 값은 어떤 값이 되어도 상관 없습니다.
(pivot 값에 따라 시간 복잡도가 달라집니다)
-퀵정렬 코드(난수x)
int Partition(int* arr, int low, int high, int n) {
int pivot = arr[size_t(floorf((high - low) / 2.0f)) + low];
int i = low;
int j = high;
while (true) {
while (arr[i] < pivot) i++;
while (arr[j] > pivot) j--;
if (i >= j) return j;
std::swap(arr[i], arr[j]);
}
}
void QuickSort(int* arr, int low, int high, int n) {
if (low >= 0 && high >= 0 && low < high) {
int p = Partition(arr, low, high, n);
QuickSort(arr, low, p, n);
QuickSort(arr, p + 1, high, n);
}
}
-퀵정렬 코드(난수)
int Partition(std::vector<int>& v, int low, int high) {
std::cout << "Pivot = " << v[high] << '\n';
int x = v[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (v[j] <= x) {
i++;
std::swap(v[i], v[j]);
}
}
std::swap(v[i + 1], v[high]);
Print(v, low, high);
return i + 1;
}
int RandomizedPartition(std::vector<int>& v, int low, int high) {
int random = low + rand() % (high - low + 1);
std::swap(v[random], v[high]);
return Partition(v, low, high);
}
void RandomizedQuicksort(std::vector<int>& v, int low, int high) {
Print(v, low, high);
if (low < high) {
int mid = RandomizedPartition(v, low, high);
RandomizedPartition(v, low, mid - 1);
RandomizedPartition(v, mid + 1, high);
}
}
-퀵정렬 성능분석)
무작위 pivot값을 사용하는 퀵정렬에 대해 분석해보겠습니다.
우선, 퀵정렬의 성능은 크기 비교 횟수를 기준으로 분석할 수 있다고 보조 명제를 하나 설정하겠습니다.
퀵정렬은 pivot값을 기준으로 분할하는 정렬이기 떄문에
분할 함수를 호출하는 횟수는 n에 비례해서 많아집니다.
분할이 어떻게 되느냐에 따라 (pivot 을 어떻게 설정하느냐에 따라) 성능이 많이 달라집니다.
분할이 균등하게 되면 비교 횟수도 확연히 줄어들기 때문에, 비교 횟수를 기준으로 퀵정렬의 성능을 분석할 수 있습니다.
(비교 횟수가 줄어들면 분할이 균등하게 되었다는 의미)
아래에서의 X는 비교 횟수를 의미합니다.

그리고, 보조명제를 몇 개 추가하겠습니다.

편의를 위해 중복이 없다고 가정하겠습니다.
void RandomizedQuicksort(std::vector<int>& v, int low, int high) {
Print(v, low, high);
if (low < high) {
int mid = RandomizedPartition(v, low, high);
RandomizedPartition(v, low, mid - 1);
RandomizedPartition(v, mid + 1, high);
}
}한 번 pivot 값으로 지정되면 다시는 pivot 값이 될 수 없습니다.
int Partition(std::vector<int>& v, int low, int high) {
std::cout << "Pivot = " << v[high] << '\n';
int x = v[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (v[j] <= x) {
i++;
std::swap(v[i], v[j]);
}
}
std::swap(v[i + 1], v[high]);
Print(v, low, high);
return i + 1;
}모든 값은 pivot값과 비교되는 구조이고 비교는 1번만 가능합니다.
이제 기댓값이라는 것에 대해 알아보겠습니다.
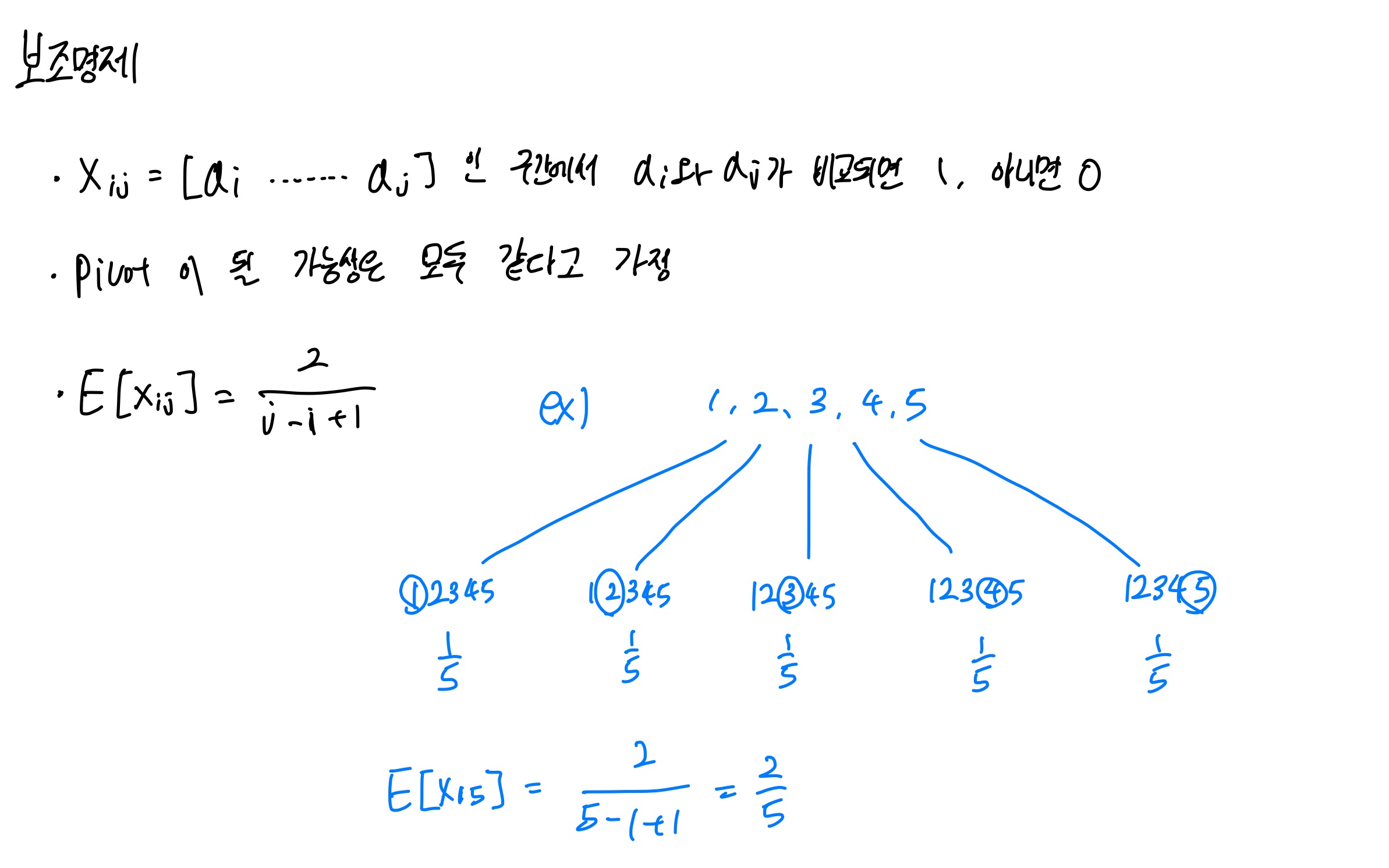
1,2,3,4,5 배열이 있을 때, pivot으로 선택될 확률은 1/5 입니다.
이를 E[Xij] 로 구간화하면 위와 같은 기댓값을 구하는 식이 나오게 됩니다. 이 식을 가지고 퀵정렬 비교횟수의 기댓값을 구해보겠습니다.
구하기 전에 알아야 할 지식이 하나 더 있습니다.
바로 조화급수입니다.
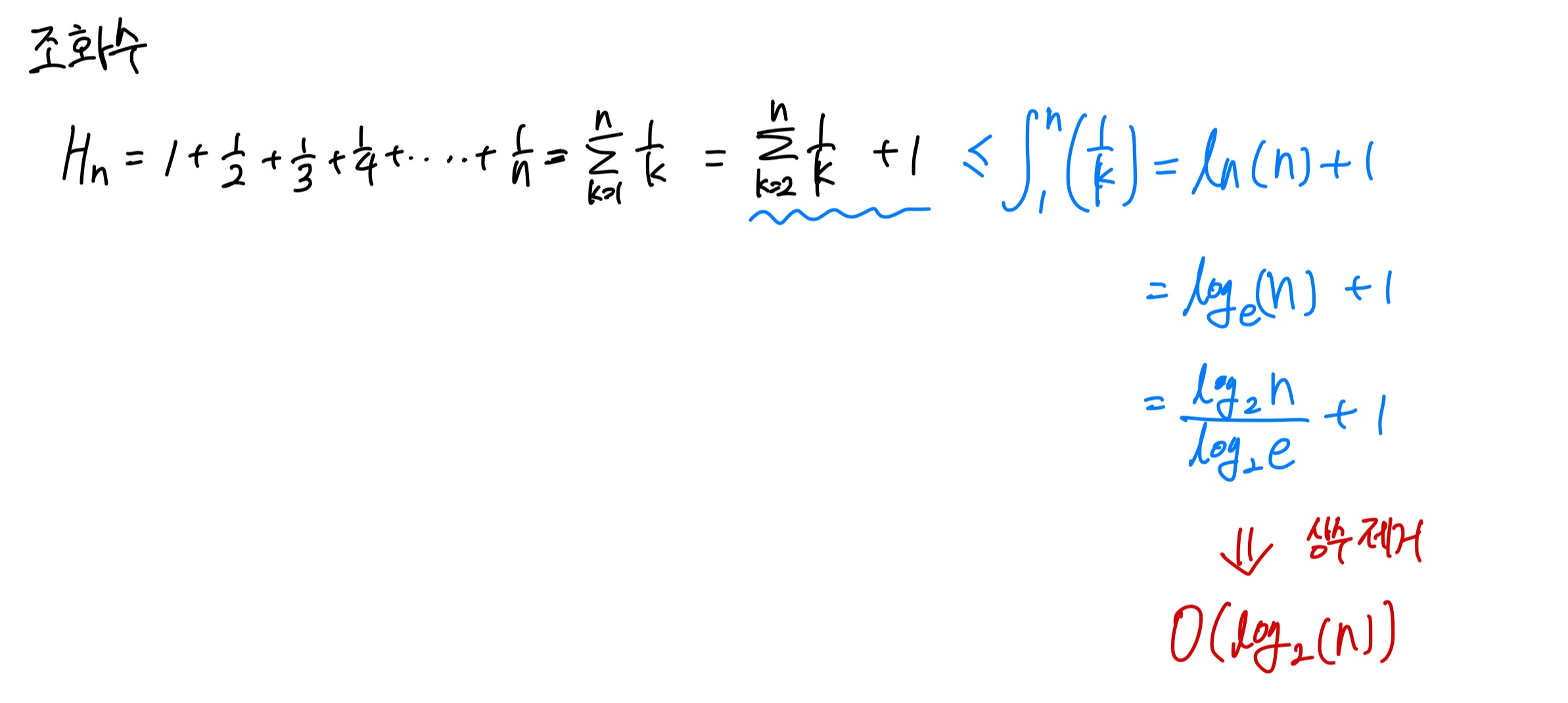
급수의 성질과 적분의 성질을 약간 이용한 것입니다.
적분값 = 면적의 넓이 이기 때문에 상한이라는 점을 이용해서 Big-O notation 으로 유도할 수 있습니다.
이제 조화수의 성질을 가지고 퀵정렬 비교횟수 기댓값의 상한을 살펴보겠습니다.

시그마가 두 개 겹쳐있는 모습은 프로그래밍에서 흔히 볼수 있는 이중OO문 을 생각하시면 편합니다.
조화수의 성질과 적분의 성질을 이용하면 E(x)의 상한을 구할 수 있습니다.
그리고 상수와 차수가 낮은 부분들을 제거해주면 결론적으로 퀵정렬의 평균적인 기대 성능은 O(nlog(n)) 이라는 것을 확인할 수 있습니다.
'DataStructure > Algorithm' 카테고리의 다른 글
| Bucket Sort (버킷 정렬) (0) | 2024.09.23 |
|---|---|
| 3-way QuickSort (3분할 퀵정렬) (0) | 2024.09.16 |
| MergeSort (병합 정렬) (2) | 2024.09.15 |
| Sequential Search vs Binary Search ( 순차 탐색 vs 이진 탐색) (0) | 2024.09.13 |
| 마스터 정리와 증명 (2) | 2024.09.12 |